Lemniskata Bernoulliego

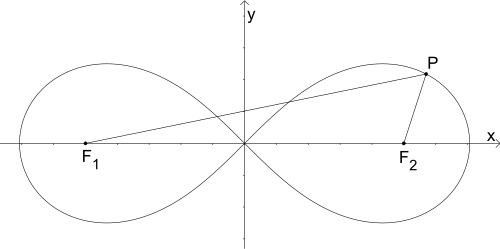
Lemniskata Bernoulliego – krzywa płaska będąca zbiorem punktów, dla których iloczyn odległości od dwóch ustalonych punktów (ognisk lemniskaty) oddalonych o ${\displaystyle 2a}$ jest stały i równy ${\displaystyle a^{2}.}$ Lemniskata Bernoulliego jest szczególnym przypadkiem owalu Cassiniego^[1].

Została ona opisana przez Jakoba Bernoulliego w 1694 roku^[1], w czasopiśmie naukowym „Acta Eruditorum”.

Równania lemniskaty:

• we współrzędnych kartezjańskich^[1]:

  ${\displaystyle (x^{2}+y^{2})^{2}=2a^{2}(x^{2}-y^{2}),}$

• we współrzędnych biegunowych^[1]:

  ${\displaystyle r^{2}=2a^{2}\cos 2\varphi ,}$

• równanie parametryczne:

  ${\displaystyle x={\frac {a{\sqrt {2}}\cos t}{1+\sin ^{2}t}},\quad y={\frac {a{\sqrt {2}}\sin t\cos t}{1+\sin ^{2}t}},}$    gdzie ${\displaystyle t\in [0,2\pi ).}$

Początek układu współrzędnych jest punktem rozgałęzienia. W punkcie tym są punkty przegięcia; równanie stycznych w tym punkcie: ${\displaystyle y=\pm x.}$ Przecięcie z osią ${\displaystyle Ox{:}}$ ${\displaystyle A,C(\pm a{\sqrt {2}},0);}$ ekstrema: ${\displaystyle \pm {\frac {1}{2}}a{\sqrt {3}}}$ oraz ${\displaystyle \pm {\frac {1}{2}}a}$ o argumentach ${\displaystyle \varphi =\pm {\frac {1}{6}}\pi .}$

Promień krzywizny ${\displaystyle r=2a^{2}\!/3\rho .}$

Pole powierzchni obu obszarów ograniczonych krzywą wynosi ${\displaystyle 2a^{2}}$^[2].

• lemniskata Bootha
• lista krzywych

• Bernoulli lemniscate (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2025-04-23].