Sprzężenie izotomiczne

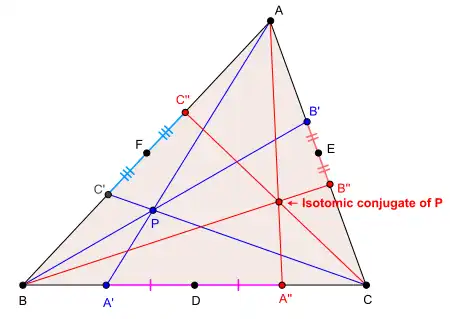
Sprzężenie izotomiczne punktu w trójkącie to inny punkt, określony jednoznacznie poprzez trójkąt oraz położenie punktu wyjściowego punktu.

Niech dany będzie trójkąt ${\displaystyle \Delta ABC}$ oraz punkt ${\displaystyle P}$ wewnątrz niego. Poprowadźmy półproste wychodzące z wierzchołków trójkąta, przecinające przeciwległe boki (tzw. czewiany) i przechodzące poprzez punkt ${\displaystyle P.}$ Oznaczmy poprzez ${\displaystyle A',B',C'}$ ich przecięcie z odpowiednimi bokami trójkąta. Odbijmy każdy z punktów ${\displaystyle A',B',C'}$ poprzez środki odpowiednich boków trójkąta i oznaczmy obrazy tych punktów poprzez ${\displaystyle A'',B'',C''.}$ Poprowadźmy teraz proste ${\displaystyle AA'',BB'',CC''.}$ Z twierdzenia odwrotnego do twierdzenia Cevy, proste te również przetną się w jednym punkcie ${\displaystyle P'}$ (jako że długości odcinków na które punkty ${\displaystyle A',B',C'}$ oraz ${\displaystyle A'',B'',C''}$ dzielą boki są takie same)^[1][2]. Punkt ten nazywamy sprzężeniem izotomicznym punktu ${\displaystyle P}$.

Ponadto, proste ${\displaystyle AA'',BB'',CC''}$ nazywane są prostymi izotomicznymi^[1] do prostych ${\displaystyle AA',BB',CC',}$ a punkty ${\displaystyle A'',B'',C''}$ punktami izotomicznymi do punktów ${\displaystyle A',B',C'}$^[3].

Jeśli oznaczmy długości boków trójkąta poprzez ${\displaystyle a,b,c,}$ a współrzędne trójliniowe punktu ${\displaystyle P}$ poprzez ${\displaystyle p:q:r,}$ to współrzędne sprzężenia izotomicznego punktu ${\displaystyle P}$ wynoszą

${\displaystyle a^{-2}p^{-1}:b^{-2}q^{-1}:c^{-2}r^{-1}.}$

Punkty o współrzędnych barycentrycznych ${\displaystyle (x,y,z)}$ oraz ${\displaystyle (x',y',z')}$ są sprzężone izotomicznie, gdy zachodzi^[4][5]

${\displaystyle xx'=yy'=zz'.}$

Z definicji, jeśli ${\displaystyle P'}$ jest sprzężeniem izotomicznym punktu ${\displaystyle P,}$ to sprzężeniem punktu ${\displaystyle P'}$ będzie sam punkt ${\displaystyle P.}$

Sprzężeniem izotomicznym centroidu trójkąta (przecięcia wszystkich środkowych) jest z definicji sam centroid^[6].

Poniższe pary punktów są względem siebie sprzężone izotomicznie:

• punktu Nagela oraz punkt Gergonne'a^[2][6][7],
• trzeci punkt Brocarda i punkt przecięcia symedian (zwany punktem Lemoine’a)^[8],
• ortocentrum trójkąta i punkt przecięcia symedian jego trójkąta antydopełniającego^[9].

• sprzężenie izogonalne

• O. Bottema: Topics in Elementary Geometry. Springer, 2008.

• Eric W.E.W. Weisstein Eric W.E.W., Isotomic Conjugate., [w:] MathWorld, Wolfram Research  (ang.).
• John Casey: A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions with Numerous Examples. Dublin: Hodges, Figgis, Co., 1893.
• Theory of Isogonal and Isotomic Points, and of Antiparallel and Symmedian Lines.. W: John Casey: A Sequel to the First Six Books of the Elements of Euclid, Containing an Easy Introduction to Modern Geometry with Numerous Examples. Wyd. 3. Dublin: Hodges, Figgis, Co., 1886.
• Robert Lachlan: An Elementary Treatise on Modern Pure Geometry. Macmillan and Co., 1893. Brak numerów stron w książce
• Paul Yiu: Notes on Euclidean Geometry. 1998.
• S.I. Zetel: Geometria trójkąta. Andrzej Mąkowski (tłum.). Warszawa: Państwowe Zakłady Wydawnictw Szkolnych, 1964.