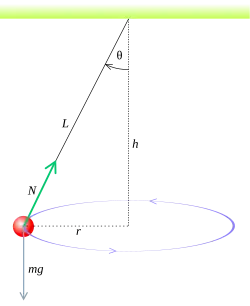
Wahadło stożkowe

Wahadło stożkowe – punktowa masa zawieszona na nierozciągliwej nici zamocowanej w punkcie znajdująca się w polu sił grawitacyjnych. Masa obraca się wokół osi równowagi wahadła, co odpowiada temu, że nić tworzy z osią pionową cały czas taki sam kąt.

Wahadło jest szczególnym przypadkiem wahadła sferycznego.

Na nieważkiej nici o długości ${\displaystyle L}$ zawieszone jest ciało o masie ${\displaystyle m,}$ zataczając poziomy okrąg ze stałą prędkością ${\displaystyle \upsilon .}$ Nić tworzy cały czas z pionem kąt ${\displaystyle \theta }$^[1].

Na ciało działają dwie siły: naciąg nici ${\displaystyle (N)}$ i siła ciężkości ${\displaystyle (mg).}$

• Składowa pionowa siły ${\displaystyle N}$ równoważy przyciąganie grawitacyjne (siłę ciężkości)

  ${\displaystyle N\cos \theta =mg.}$

• Składowa pozioma siły ${\displaystyle N}$ jest siłą dośrodkową w ruchu po okręgu

  ${\displaystyle N\sin \theta ={\frac {mv^{2}}{r}}}$

gdzie ${\displaystyle r=L\sin \theta .}$

Z powyższych równań wynika:

${\displaystyle {\frac {g}{\cos \theta }}={\frac {v^{2}}{r\sin \theta }}.}$

Ponieważ ${\displaystyle v=\omega r}$ (związek między prędkością liniową a kątową), przy czym ${\displaystyle \omega ={\frac {2\pi }{T}}}$ to można powyższe zapisać jako

${\displaystyle {\frac {g}{\cos \theta }}={\frac {({\frac {2\pi r}{T}})^{2}}{r\sin \theta }},}$

${\displaystyle {\frac {g}{\cos \theta }}={\frac {(2\pi )^{2}r}{T^{2}\sin \theta }},}$

stąd

${\displaystyle T=2\pi {\sqrt {{\frac {r}{\sin \theta }}{\frac {\cos \theta }{g}}}}=2\pi {\sqrt {\frac {L\cos \theta }{g}}}}$

oraz

${\displaystyle \omega ={\sqrt {\frac {g}{L\cos \theta }}}.}$

Dla małych kątów ${\displaystyle \theta ,}$ ${\displaystyle \cos(\theta )\approx 1,}$ wówczas okres ruchu wahadła ${\displaystyle T}$ wahadła stożkowego nie zależy od kąta wahadła i jest taki sam jak dla wahadła matematycznego o tej samej długości.