Zapis wektorowy
W zapisie wektorowym wzory Freneta mają następującą postać




gdzie[1]:
 – parametr naturalny krzywej (długość łuku),
– parametr naturalny krzywej (długość łuku), – wektor wodzący punktu na krzywej,
– wektor wodzący punktu na krzywej, – wektor styczny,
– wektor styczny, – wektor normalnej głównej,
– wektor normalnej głównej, – wektor binormalny,
– wektor binormalny, – wektor krzywizny,
– wektor krzywizny, – promień krzywizny,
– promień krzywizny, – krzywizna krzywej,
– krzywizna krzywej, – promień torsji krzywej (promień drugiej krzywizny),
– promień torsji krzywej (promień drugiej krzywizny), – torsja krzywej (druga krzywizna),
– torsja krzywej (druga krzywizna), – wektory normalne płaszczyzn: ściśle stycznej i prostującej.
– wektory normalne płaszczyzn: ściśle stycznej i prostującej.
Z punktem  na krzywej przestrzennej
na krzywej przestrzennej  można związać dwa lokalne układy ortogonalnych osi liczbowych. Pierwszy z nich jest nieruchomy, prawoskrętny i określony przez wersory
można związać dwa lokalne układy ortogonalnych osi liczbowych. Pierwszy z nich jest nieruchomy, prawoskrętny i określony przez wersory  Drugi prawoskrętny układ wersorów
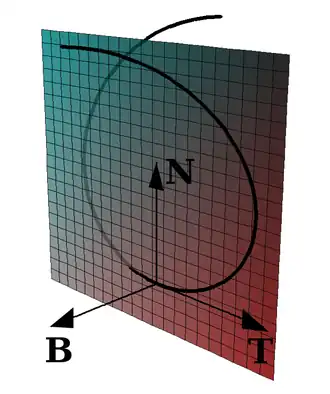
Drugi prawoskrętny układ wersorów  jest związany z krzywą i określa trzy istotne kierunki: styczny, normalny i binormalny. Dwa pierwsze wyznaczone są przez wersory
jest związany z krzywą i określa trzy istotne kierunki: styczny, normalny i binormalny. Dwa pierwsze wyznaczone są przez wersory
| |
 
|
|
(1.1) |
gdzie:
| |  |
|
(1.2) |
a trzeci jest definiowany[1] wzorem
| |
![{\displaystyle {\begin{aligned}\mathbf {b} &=\mathbf {t} \times \mathbf {n} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\x^{'}&y^{'}&z^{'}\\\rho x^{''}&\rho y^{''}&\rho z^{''}\end{vmatrix}}\\[1ex]&=\rho {\Big [}(y^{'}z^{''}-z^{'}y^{''})\,\mathbf {i} +(z^{'}x^{''}-x^{'}z^{''})\,\mathbf {j} \\[1ex]&\quad +(x^{'}y^{''}-y^{'}x^{''})\,\mathbf {k} {\Big ]}\\[1ex]&=\rho \,{\big (}A\,\mathbf {i} +B\,\mathbf {j} +C\,\mathbf {k} {\big )}=\rho \mathbf {H} .\end{aligned}}}](./d9f00eebe39b63c559b353f9f07e4abfdff7aeb2.svg)
|
|
(1.3) |
Jeżeli krzywa  leży na płaszczyźnie
leży na płaszczyźnie  o normalnej
o normalnej  to wektor binormalnej
to wektor binormalnej  do tej krzywej w każdym jej punkcie jest stały i
do tej krzywej w każdym jej punkcie jest stały i  Płaszczyzna
Płaszczyzna  jest w tym przypadku płaszczyzną ściśle styczną dla dowolnego punktu krzywej
jest w tym przypadku płaszczyzną ściśle styczną dla dowolnego punktu krzywej 
W analizie przestrzennych właściwości krzywych istotną rolę odgrywają pochodne wersorów krawędzi trójścianu Freneta.
Na podstawie wzoru (1.1) mamy
| |

|
|
(1.4) |
i różniczkując wzór (1.3), otrzymujemy
| |

|
|
(1.5) |
ponieważ  i
i  są kolinearne. Ponadto z (1.5) wynika, że
są kolinearne. Ponadto z (1.5) wynika, że  a ponieważ również
a ponieważ również 
więc
| |

|
|
(1.6) |
gdzie  jest torsją krzywej w punkcie
jest torsją krzywej w punkcie  określoną wzorem (1.8).
określoną wzorem (1.8).
Teraz można już obliczyć pochodną normalnej głównej, korzystając ze wzoru 
| |
![{\displaystyle {\begin{aligned}\mathbf {n} ^{'}&=-(\mathbf {t} \times \mathbf {b} )^{'}=-\mathbf {t} ^{'}\!\times \mathbf {b} -\mathbf {t} \times \mathbf {b} ^{'}\\[1ex]&=-{\frac {1}{\rho }}\,\mathbf {n} \times \mathbf {b} -{\frac {1}{\tau }}\mathbf {t} \times \mathbf {n} \\[1ex]&=-{\frac {1}{\rho }}\,\mathbf {t} -{\frac {1}{\tau }}\mathbf {b} =-\kappa \mathbf {t} -T\mathbf {b} .\end{aligned}}}](./e70e4b3599a487d7c1c7d51d155e88f531065a3c.svg)
|
|
(1.7) |
Poniższa tabelka zawiera kosinusy kierunkowe wersorów Freneta osi stycznej, normalnej i binormalnej z kierunkami osi 
| x | y | z |
 |  |  |  |
 |  |  |  |
 |  |  |  |
Wzory dla pochodnych wersorów Freneta zestawiono poniżej[1].
|  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
Torsję krzywej można obliczyć, korzystając ze wzoru (1.6) po uwzględnieniu (1.1) i (1.5)
| |
![{\displaystyle {\begin{aligned}T&={\frac {1}{\tau }}=\mathbf {b} ^{'}\cdot \mathbf {n} =\\[1ex]&=(\mathbf {t} \times \mathbf {n} ^{'})\cdot \mathbf {n} ={\big [}\mathbf {t} \times (\rho \mathbf {N} )^{'}{\big ]}\cdot \rho \mathbf {N} =\\[1ex]&={\big [}\mathbf {t} \times (\rho ^{'}\mathbf {N} +\rho \mathbf {N} ^{'}){\big ]}\cdot \rho \mathbf {N} =\\[1ex]&=\rho ^{2}(\mathbf {t} \times \mathbf {N} ^{'})\cdot \mathbf {N} =-\rho ^{2}(\mathbf {r} ^{'}\times \mathbf {r} ^{''})\cdot \mathbf {r} ^{'''}=\\[1ex]&=-\rho ^{2}\;{\begin{vmatrix}x^{'}&y^{'}&z^{'}\\x^{''}&y^{''}&z^{''}\\x^{'''}&y^{'''}&z^{'''}\end{vmatrix}},\end{aligned}}}](./1f9e3cfc84a4f996623437f3e86de05b2b062972.svg)
|
|
(1.8) |
dzięki temu, że 
Torsja  określona w dowolnym punkcie
określona w dowolnym punkcie  krzywej
krzywej  wzorem
wzorem  stanowi pewną miarę zwichrowania tej krzywej w bliskim otoczeniu punktu
stanowi pewną miarę zwichrowania tej krzywej w bliskim otoczeniu punktu  Polega ono na wychylaniu się krzywej z jej płaszczyzny ściśle do niej stycznej w tym punkcie. Gdy torsja ma wartość zerową krzywa w otoczeniu punktu
Polega ono na wychylaniu się krzywej z jej płaszczyzny ściśle do niej stycznej w tym punkcie. Gdy torsja ma wartość zerową krzywa w otoczeniu punktu  jest płaska, bez zwichrowania.
jest płaska, bez zwichrowania.
Zapis parametryczny
Dana jest krzywa przestrzenna  opisana parametrycznie równaniami[2]
opisana parametrycznie równaniami[2]
| |

|
|
(1) |
Na tej krzywej wyróżnimy dwa punkty 
 odpowiadające dwom wartościom
odpowiadające dwom wartościom  parametru
parametru  Przez te punkty przechodzi sieczna opisana równaniem
Przez te punkty przechodzi sieczna opisana równaniem
| |

|
|
(2) |
Dzieląc mianowniki przez  i przechodząc do granicy
i przechodząc do granicy  otrzymujemy równanie linii stycznej do krzywej
otrzymujemy równanie linii stycznej do krzywej  w punkcie
w punkcie 
| |

|
|
(3) |
gdzie przez  oznaczono pochodne względem parametru liczone w punkcie
oznaczono pochodne względem parametru liczone w punkcie 
Równanie o postaci (3) jest konsekwencją kolinearności wektorów  i
i 
Równanie płaszczyzny normalnej  (prostopadłej) do krzywej w punkcie
(prostopadłej) do krzywej w punkcie  można zapisać w postaci[2] iloczynu skalarnego wektora stycznego do niej z dowolnym wektorem leżącym w płaszczyźnie
można zapisać w postaci[2] iloczynu skalarnego wektora stycznego do niej z dowolnym wektorem leżącym w płaszczyźnie 
| |

|
|
(4) |
Równanie płaszczyzny ściśle stycznej  do krzywej w punkcie
do krzywej w punkcie  zapiszemy w postaci
zapiszemy w postaci
| |

|
|
(5) |
Problem polega teraz na tym, aby określić współrzędne  takiego wektora
takiego wektora  który byłby prostopadły do płaszczyzny ściśle stycznej
który byłby prostopadły do płaszczyzny ściśle stycznej 
Rozważmy równanie takiej płaszczyzny  na której leży styczna i która
na której leży styczna i która
- przechodzi przez punkt
 – a zatem każdy jej wektor
– a zatem każdy jej wektor  jest prostopadły do
jest prostopadły do 
| |

|
|
(6) |
oraz
- każdy wektor
 leżący na płaszczyźnie
leżący na płaszczyźnie  jest prostopadły do
jest prostopadły do 
| |

|
|
(7) |
Wektor  jest również prostopadły do wektora stycznego
jest również prostopadły do wektora stycznego  który leży na
który leży na 
| |

|
|
(8) |
Wykorzystując wzór Taylora zamiast (7), możemy napisać
| |

|
|
(9) |
gdzie 
Po uwzględnieniu (8) i (9) otrzymujemy
| |

|
|
(10) |
Można teraz z (8) i (10) wyznaczyć niewiadome  i na podstawie (6) otrzymuje się, po przejściu do granicy
i na podstawie (6) otrzymuje się, po przejściu do granicy 
| |

|
|
(11) |
Tak więc wektor  prostopadły do płaszczyzny ściśle stycznej ma współrzędne
prostopadły do płaszczyzny ściśle stycznej ma współrzędne
| |
 |
|
(12) |
Przez punkt  krzywej
krzywej  przechodzą trzy wzajemnie prostopadłe płaszczyzny tworzące trójścian Freneta[3]:
przechodzą trzy wzajemnie prostopadłe płaszczyzny tworzące trójścian Freneta[3]:
- ściśle styczna (o wektorze normalnym
 ) – równanie (5) i (12),
) – równanie (5) i (12),
- normalna (o wektorze normalnym
 ) – równanie (4),
) – równanie (4),
- prostująca (o wektorze normalnym
 ) – prostopadła do dwu poprzednich. Jej równanie ma postać
) – prostopadła do dwu poprzednich. Jej równanie ma postać
| |

|
|
(13) |
Wektor  jest prostopadły do obydwu wektorów
jest prostopadły do obydwu wektorów  i
i  i dlatego muszą być spełnione dwa równania
i dlatego muszą być spełnione dwa równania
| |

|
|
(14) |
| |

|
|
(15) |
Rozwiązanie równań (13) i (15) ma postać wzorów
| |

|
|
(16) |
Krawędziami trójścianu Freneta są proste:
- styczna – o wersorze
 i równaniu (3),
i równaniu (3),
- normalna główna – o wersorze
 i prostopadła do płaszczyzny prostującej, określona równaniem
i prostopadła do płaszczyzny prostującej, określona równaniem
| |

|
|
(17) |
- binormalna – o wersorze
 i prostopadła do płaszczyzny ściśle stycznej, określona równaniem
i prostopadła do płaszczyzny ściśle stycznej, określona równaniem
| |

|
|
(18) |
Zachodzą przy tym następujące tożsamości
| |
 (lub (lub  ), ),
|
|
(19) |
| |
 (lub (lub  ). ).
|
|
(20) |
- Krzywizna i torsja krzywej
Płaszczyzna normalna do krzywej  w jej punkcie
w jej punkcie  opisana jest równaniem
opisana jest równaniem
| |

|
|
(21) |
gdzie  jest wektorem stycznym do krzywej w punkcie
jest wektorem stycznym do krzywej w punkcie 
Przecina ona normalną główną (17) w punkcie  o współrzędnych
o współrzędnych
| |

|
|
(22) |
Po podstawieniu (22) do (21) i uwzględnieniu (15) otrzymujemy wartość parametru
| |

|
|
(23) |
określającą położenie punktu  na kierunku normalnej głównej.
na kierunku normalnej głównej.
Po podzieleniu licznika i mianownika przez  i po przejściu do granicy
i po przejściu do granicy  otrzymujemy
otrzymujemy
| |

|
|
(24) |
Gdy punkt  dąży do punktu
dąży do punktu  punkt
punkt  dąży do punktu
dąży do punktu  o współrzędnych
o współrzędnych
| |

|
|
(25) |
Po wykorzystaniu tożsamości (19) otrzymujemy
| |

|
|
(26) |
Punkt o współrzędnych (25) nazywany jest środkiem krzywizny krzywej  w jej punkcie
w jej punkcie  Miejscem geometrycznym środków krzywizny krzywej
Miejscem geometrycznym środków krzywizny krzywej  o współrzędnych
o współrzędnych  jest krzywa
jest krzywa  zwana ewolutą krzywej
zwana ewolutą krzywej 
Odległość punktu  od punktu
od punktu  jest tak zwanym promieniem krzywizny
jest tak zwanym promieniem krzywizny  krzywej w jej punkcie
krzywej w jej punkcie  Odległość tę oblicza się na podstawie wzorów (25) po uwzględnieniu tożsamości (20)
Odległość tę oblicza się na podstawie wzorów (25) po uwzględnieniu tożsamości (20)
![{\displaystyle {\begin{aligned}\rho ^{2}&=(x_{*}-x_{o})^{2}+(y_{*}-y_{o})^{2}+(z_{*}-z_{o})^{2}\\[1ex]&=L^{2}\lambda _{o}^{2}+M^{2}\lambda _{o}^{2}+N^{2}\lambda _{o}^{2}=\lambda _{o}^{2}(L^{2}+M^{2}+N^{2}),\end{aligned}}}](./0f88eb63c142400a2a439117fc18362e6f31be2d.svg)
| |

|
|
(27) |
Krzywiznę krzywej określa wzór
| |

|
|
(28) |
Krzywizna  nazywana jest pierwszą krzywizną krzywej dla odróżnienia jej od drugiej krzywizny
nazywana jest pierwszą krzywizną krzywej dla odróżnienia jej od drugiej krzywizny  nazywanej torsją krzywej. Torsja
nazywanej torsją krzywej. Torsja  jest miarą skrętu krzywej związanego z obrotem trójścianu Freneta dokoła osi stycznej. Obrót ten można obliczyć, wprowadzając do rozważań jednostkowy wektor
jest miarą skrętu krzywej związanego z obrotem trójścianu Freneta dokoła osi stycznej. Obrót ten można obliczyć, wprowadzając do rozważań jednostkowy wektor


| |

|
|
(29) |
dzięki któremu torsję  można zdefiniować wzorem
można zdefiniować wzorem
| |

|
|
(30) |
przy czym
| |

|
|
(31) |
dzięki temu, że po uwzględnieniu tożsamości Lagrange’a
| |
![{\displaystyle {\begin{aligned}\mathbf {H} ^{2}&=A^{2}+B^{2}+C^{2}=\\[1ex]&=(y^{'}z^{''}-z^{'}y^{''})^{2}+(x^{'}z^{''}-z^{'}x^{''})^{2}+(x^{'}y^{''}-y^{'}x^{''})^{2}=\\[1ex]&=(x^{'2}+y^{'2}+z^{'2})(x^{''2}+y^{''2}+z^{''2})-\\[1ex]&\qquad -(x^{'}x^{''}+y^{'}y^{''}+z^{'}z^{''})^{2}=\\&=\mathbf {t} ^{2}\mathbf {N} ^{2}-(\mathbf {t} \cdot \mathbf {N} )^{2}=(\mathbf {t} \cdot \mathbf {t} )(\mathbf {N} \cdot \mathbf {N} )-0={\tfrac {1}{\rho ^{2}}}.\end{aligned}}}](./aa2640cc05adaf223020ebcca1d2bf3daaf2655e.svg)
|
|
(32) |
Na podstawie (31) i dzięki temu, że  otrzymujemy
otrzymujemy
| |
![{\displaystyle {\begin{aligned}T&=(\mathbf {h} ^{'}\cdot \,\mathbf {n} )=\\[1ex]&=\rho ^{2}{\Big (}|\mathbf {H} |(\mathbf {H} ^{'}\mathbf {\cdot } \,\mathbf {n} )-|\mathbf {H} |^{'}(\mathbf {H} \cdot \mathbf {n} ){\Big )}=\\[1ex]&=\rho ^{2}|\mathbf {H} |(\mathbf {H} ^{'}\cdot \mathbf {n} )=\rho (\mathbf {H} ^{'}\cdot \mathbf {n} )=\\[1ex]&=\rho ^{2}(\mathbf {H} ^{'}\cdot \mathbf {N} )=-\rho ^{2}{\begin{vmatrix}x^{'}&y^{'}&z^{'}\\x^{''}&y^{''}&z^{''}\\x^{'''}&y^{'''}&z^{'''}\end{vmatrix}}.\end{aligned}}}](./ef88cb1cdecaf1bde30da042830f6bf4f5069e94.svg)
|
|
(33) |
Przykłady
1. Elipsa








 - ponieważ
- ponieważ 
2. Okrąg na płaszczyźnie o normalnej: 







 - ponieważ
- ponieważ 
3. Spirala na walcu kołowym, linia śrubowa – krzywa „nawinięta” na walec o promieniu  Spirala jest prawoskrętna wokoło osi
Spirala jest prawoskrętna wokoło osi 




gdzie  jest kątem nachylenia stycznej do osi pręta względem płaszczyzny
jest kątem nachylenia stycznej do osi pręta względem płaszczyzny  kołowego przekroju walca,
kołowego przekroju walca,



stąd





4. Parabola płaska









5. Parabola przestrzenna










Zerowanie się torsji wynika również bezpośrednio z faktu, że  Rozważana krzywa w całości leży na swojej płaszczyźnie ściśle stycznej o normalnej
Rozważana krzywa w całości leży na swojej płaszczyźnie ściśle stycznej o normalnej 
6. Spirala Archimedesa









![{\displaystyle {}\qquad =\left[0,\;0,\;{\tfrac {a^{2}\sigma }{\alpha }}\scriptstyle {(t^{2}+2)}\right]=(0,\,0,\,1),}](./07f85374f6be092c654ea885773208d82f373eef.svg)

7. Spirala stożkowa – krzywa „nawinięta” na stożek kołowy.





![{\displaystyle x^{'}(s)={\tfrac {1}{\sigma }}[b\cos t-(a+bt)\sin t],}](./5ab26748a3aeb1a7e1e235cabaa31548cd56fec4.svg)
![{\displaystyle y^{'}(s)={\tfrac {1}{\sigma }}[b\sin t+(a+bt)\cos t],\quad z^{'}(s)={\tfrac {h}{\sigma }},}](./80b04a474d814787125cb049a766392203712725.svg)


![{\displaystyle \mu =(\sigma ^{2}+b^{2})(a+bt),\;\;\nu =b[2\sigma ^{2}-(a+bt)^{2}],}](./da13c813151670316c9d63b63d64928a534b6008.svg)

![{\displaystyle \mathbf {b} =\mathbf {t} \times \mathbf {n} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\{\frac {1}{\sigma }}\scriptstyle {[(b\cos t-(a+bt)\sin t]}&{\frac {1}{\sigma }}\scriptstyle {[b\sin t+(a+bt)\cos t]}&{\tfrac {h}{\sigma }}\\-{\tfrac {1}{\kappa }}\scriptstyle {(\mu \cos t+\nu \sin t)}&{\tfrac {1}{\kappa }}\scriptstyle {(\nu \cos t-\mu \sin t)}&-{\tfrac {bh}{\kappa }}\scriptstyle {(a+bt)}\end{vmatrix}}=}](./a132f054d0b953e3b6ca0e0cbddbeffc31f411bd.svg)
![{\displaystyle =\{{\tfrac {h\sigma }{\kappa }}\scriptstyle {[-2b\cos t+(a+bt)\sin t]},\;\;-{\tfrac {h\sigma }{\kappa }}\scriptstyle {[(a+bt)\cos t+2b\sin t]},\;\;{\tfrac {\sigma }{\kappa }}\scriptstyle {[2b^{2}+(a+bt)^{2}]}\;\},}](./1d819a498068efc57773de1e6bae8cd690d9eb84.svg)



![{\displaystyle z^{'''}(s)=-{\tfrac {b^{2}h}{\sigma ^{7}}}[\sigma ^{2}-4(a+bt)^{2}],}](./9c03a52d103b2ff48b4adbd364a34f0cbee19687.svg)

![{\displaystyle T=-{\begin{vmatrix}{\tfrac {1}{\sigma }}\scriptstyle {[b\cos t-(a+bt)\sin t]}&{\tfrac {1}{\sigma }}\scriptstyle {[b\sin t+(a+bt)\cos t]}&{\tfrac {h}{\sigma }}\\-{\tfrac {1}{\kappa }}\scriptstyle {(\mu \cos t+\nu \sin t)}&{\tfrac {1}{\kappa }}\scriptstyle {(\nu \cos t)-\mu \sin t)}&-{\tfrac {bh}{\kappa }}\scriptstyle {(a+bt)}\\-{\tfrac {1}{\kappa \sigma ^{3}}}\scriptstyle {(\gamma \cos t-\beta \sin t)}&-{\tfrac {1}{\kappa \sigma ^{3}}}\scriptstyle {(\beta \cos t+\gamma \sin t)}&-{\tfrac {b^{2}h}{\kappa \sigma ^{3}}}\scriptstyle {[\sigma ^{2}-4(a+bt)^{2}]}\end{vmatrix}}.}](./0a5dc0006e5d64feb6b5f0c71917faf6e013e92a.svg)
8. Spirala na walcu eliptycznym – krzywa „nawinięta” na taki walec o półosiach 














![{\displaystyle z^{'''}(s)={\tfrac {\gamma }{\sigma ^{7}}}\left[{\tfrac {4\gamma }{h}}\sin ^{2}t\cos ^{2}t-\sigma ^{2}(\cos ^{2}t-\sin ^{2}t)\right].}](./3167dc15dbc3cc72ec5aee3bede9084ac2882c78.svg)
9. Sinusoida „nawinięta” na walec kołowy.











10. Cykloida









![{\displaystyle {}\qquad =\left\{0,\;\;0,\;\;{\tfrac {1}{\kappa \sigma }}[(r-c\cos t)\psi -(c\sin t)\varphi ]\right\}.}](./e9458495686339fa5a0be96ce2665054adce5fcf.svg)
Wzory Freneta w 
Wzory Freneta zostały uogólnione dla więcej wymiarowych przestrzeni euklidesowych przez C. Jordana w 1874 roku.
Przypuśćmy, że  opisuje gładką krzywą w
opisuje gładką krzywą w  sparametryzowaną przez długość łuku
sparametryzowaną przez długość łuku  oraz że pierwsze
oraz że pierwsze  pochodnych
pochodnych  jest liniowo niezależnych. Geometrycznie oznacza to, że krzywa
jest liniowo niezależnych. Geometrycznie oznacza to, że krzywa  nie zawiera się w żadnej hiperpłaszczyźnie o wymiarze
nie zawiera się w żadnej hiperpłaszczyźnie o wymiarze  (ani w żadnej płaszczyźnie o niższych wymiarach). Wektory układu Freneta są bazą ortogonalną skonstruowaną przy pomocy ortogonalizacji Grama-Schmidta wykonanej na wektorach
(ani w żadnej płaszczyźnie o niższych wymiarach). Wektory układu Freneta są bazą ortogonalną skonstruowaną przy pomocy ortogonalizacji Grama-Schmidta wykonanej na wektorach 
W szczególności, jednostkowy wektor styczny  jest pierwszym wektorem układu Freneta
jest pierwszym wektorem układu Freneta 

Wektor normalny  czasami nazywany wektorem krzywizny, wskazuje odchylenie krzywej od stycznej linii prostej. Jest zdefiniowany jako
czasami nazywany wektorem krzywizny, wskazuje odchylenie krzywej od stycznej linii prostej. Jest zdefiniowany jako

W standardowej formie, jednostkowy wektor normalny jest drugim wektorem układu Freneta  i jest zdefiniowany jako
i jest zdefiniowany jako

Wektor styczny i normalny w punkcie  definiują płaszczyznę ściśle styczną w punkcie
definiują płaszczyznę ściśle styczną w punkcie 
Pozostałe wektory układu Freneta (wektor binormalny, trinormalny itd.) są zdefiniowane w sposób analogiczny jako:

Funkcje o wartościach rzeczywistych  zdefiniowane jako:
zdefiniowane jako:

są nazywane krzywiznami uogólnionymi, przy czym symbol  oznacza iloczyn skalarny wektorów
oznacza iloczyn skalarny wektorów  i
i 
W przypadku n-wymiarowym wzory Fréneta-Serreta mają postać:
 dla
dla 
W języku macierzy wyglądają tak: