Topologia
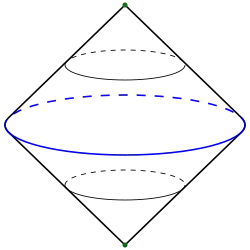 Zawieszenie okręgu (niebieskiego)
Zawieszenie okręgu (niebieskiego)
Zawieszeniem  przestrzeni topologicznej
przestrzeni topologicznej  jest przestrzeń ilorazowa powstała przez podzielenie iloczynu
jest przestrzeń ilorazowa powstała przez podzielenie iloczynu  tej przestrzeni przez przedział jednostkowy
tej przestrzeni przez przedział jednostkowy ![{\displaystyle I=[0;1]}](./27724691dc5cb75b5b3d6c91316e44470fdf6409.svg) przez relację równoważności
przez relację równoważności  [1][2]:
[1][2]:

która ściąga punkty każdej z „podstaw”  i
i  do punktu, czyli dla
do punktu, czyli dla 

Nieco mniej formalnie można to zapisać następująco:

Geometrycznie zawieszenie jest wielościanem, który można uzyskać z iloczynu  poprzez ściągnięcie do punktu każdej z podstaw:
poprzez ściągnięcie do punktu każdej z podstaw:  i
i  dla dowolnych
dla dowolnych  [2].
[2].
Kompleksy łańcuchowe
Stożkiem przekształcenia łańcuchowego  nazywamy kompleks łańcuchowy
nazywamy kompleks łańcuchowy  w którym:
w którym:

 gdzie
gdzie 
Jeśli  to kompleks
to kompleks  jest nazywany zawieszeniem i oznaczany przez
jest nazywany zawieszeniem i oznaczany przez  W kompleksie tym:
W kompleksie tym:

 [3].
[3].
Bibliografia
- Roman Duda: Wprowadzenie do topologii. Cz. I. Topologia ogólna. Warszawa: Państwowe Wydawnictwo Naukowe, 1986, seria: Biblioteka Matematyczna. Tom 61. ISBN 83-01-05714-9.
- A. Dold: Lectures on algebraic topology. Berlin Heidelberg New York: Springer Verlag, 1972.
- Marvin Greenberg: Wykłady z topologii algebraicznej. Warszawa: PWN, 1980. ISBN 83-01-00415-0.
