Algebra Clifforda

Algebra Clifforda formy kwadratowej ${\displaystyle Q\colon V\to K}$ to para ${\displaystyle (C,j),}$ gdzie ${\displaystyle C}$ jest algebrą nad ${\displaystyle K,}$ a ${\displaystyle j\colon V\to C}$ przekształceniem liniowym, taka że (dla każdego ${\displaystyle v\in V}$)

${\displaystyle (j(v))^{2}=Q(v)e_{0},}$

gdzie ${\displaystyle e_{0}\in C}$ jest elementem neutralnym mnożenia w ${\displaystyle C.}$ Oznacza się ją ${\displaystyle C\ell (V,Q).}$

Algebra Clifforda stanowi uogólnienie liczb zespolonych, kwaternionów i wielu innych podobnych konstrukcji algebraicznych.

Algebra Clifforda formy kwadratowej ${\displaystyle Q\colon V\to K}$ to para ${\displaystyle (C,j),}$ gdzie ${\displaystyle C}$ jest algebrą nad ${\displaystyle K,}$ a ${\displaystyle j\colon V\to C}$ przekształceniem liniowym, taka że (dla każdego ${\displaystyle v\in V}$)

${\displaystyle (j(v))^{2}=Q(v)e_{0},}$

gdzie ${\displaystyle e_{0}\in C}$ jest elementem neutralnym mnożenia w ${\displaystyle C,}$ przy czym spełniona jest następująca własność uniwersalności: dla każdej algebry ${\displaystyle A}$ nad ciałem ${\displaystyle K}$ i dla każdego przekształcenia liniowego ${\displaystyle i\colon V\to A,}$ które spełnia równanie

${\displaystyle (i(v))^{2}=Q(v)e_{0}'}$

(dla każdego ${\displaystyle v\in V}$) istnieje dokładnie jeden homomorfizm algebr ${\displaystyle h\colon C\to A,}$ taki że ${\displaystyle i=h\circ j,}$ tzn. taki, że poniższy diagram

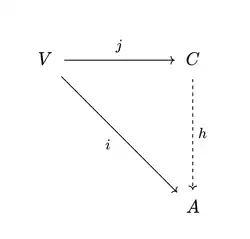
jest przemienny.

(1) Ponieważ każdej formie kwadratowej ${\displaystyle Q\colon V\to K}$ odpowiada wzajemnie jednoznacznie symetryczna forma dwuliniowa ${\displaystyle F\colon V\times V\to K}$ taka, że ${\displaystyle Q(v)=F(v,v),}$ to równość z definicji można zapisać także

${\displaystyle (j(v))^{2}=F(v,v)e_{0}.}$

(2) Rozpisując z jednej strony

${\displaystyle F(v+w,v+w)=F(v,v)+F(w,w)+2F(v,w),}$

a z drugiej strony

${\displaystyle (j(v+w))^{2}=(j(v)+j(w))^{2}=(j(v))^{2}+(j(w))^{2}+j(v)j(w)+j(w)j(v)}$

i usuwając zbędne wyrazy, dostaje się

${\displaystyle j(v)j(w)+j(w)j(v)=2F(v,w)e_{0}.}$

(3) Formę kwadratową ${\displaystyle Q}$ na skończenie wymiarowej przestrzeni ${\displaystyle V}$ z wymiarem równym ${\displaystyle n=p+q}$ da się zawsze sprowadzić do postaci

${\displaystyle Q(v)=F(v,v)=\sum _{i,j=1}^{n}\eta _{i,j}v_{i}v_{j}=v_{1}^{2}+\ldots +v_{p}^{2}-v_{p+1}^{2}-\ldots -v_{p+q}^{2},}$

gdzie ${\displaystyle \eta _{i,j}=\pm 1}$ dla ${\displaystyle i=j}$ i ${\displaystyle 0}$ poza tym.

W bazie ${\displaystyle (e_{i}),}$ w której ${\displaystyle Q,}$ ma to przedstawienie mamy (oznaczając ${\displaystyle j(v)}$ przez ${\displaystyle v}$)

${\displaystyle e_{i}e_{j}+e_{j}e_{i}=2\eta _{i,j}e_{0}.}$

Z tego powodu algebrę Clifforda formy ${\displaystyle Q\colon V\to K}$ oznacza się też ${\displaystyle C\ell _{p,q}(K).}$

(4) Wektory z ${\displaystyle V}$ utożsamia się z ich obrazami w ${\displaystyle j(V)}$ i bardzo często pisze się ${\displaystyle v}$ zamiast ${\displaystyle j(v).}$ Wektory z ${\displaystyle C\ell (V,Q)}$ rozpięte przez ${\displaystyle e_{0}}$ utożsamia się z elementami ciała ${\displaystyle K.}$

Jeżeli przestrzeń liniowa ${\displaystyle V}$ jest skończenie wymiarowa z wymiarem równym ${\displaystyle n}$ z bazą ${\displaystyle (e_{i})}$ to bazę algebry Clifforda ${\displaystyle C\ell (V,Q)}$ stanowią ${\displaystyle e_{0}}$ oraz iloczyny (${\displaystyle j(v)}$ oznaczamy przez ${\displaystyle v}$)

${\displaystyle e_{i_{1}}\ldots e_{i_{k}}}$

gdzie ${\displaystyle 1\leqslant i_{1}<\ldots <i_{k}\leqslant n,\ 1\leqslant k\leqslant n}$^[1] .

Wynika z tego, że wymiar algebry Clifforda wynosi

${\displaystyle {\binom {n}{0}}+{\binom {n}{1}}+\ldots +{\binom {n}{n}}=2^{n}.}$

Definicja algebry Clifforda jest abstrakcyjna i niekonstruktywna, jednakże algebra Clifforda dowolnej formy kwadratowej ${\displaystyle Q\colon V\to K}$ może zostać skonstruowana w następujący sposób^[1] . Niech ${\displaystyle \otimes V:=\bigoplus _{k=0}^{\infty }V^{\otimes k}}$ będzie algebrą tensorową. ${\displaystyle V^{\otimes k}:=V\otimes \ldots \otimes V}$ oznacza tutaj ${\displaystyle k}$-krotny iloczyn tensorowy ${\displaystyle V}$ ${\displaystyle (V^{\otimes 0}:=K).}$ W ${\displaystyle \otimes V}$ wybieramy ideał ${\displaystyle I}$ generowany przez tensory postaci ${\displaystyle v\otimes v-Q(v)e_{0}.}$ Algebrę ${\displaystyle C}$ definiujemy jako iloraz

${\displaystyle C:=\otimes V/I.}$

${\displaystyle C}$ wraz z naturalnym włożeniem ${\displaystyle j\colon V\to C}$ danym wzorem

${\displaystyle j(v):=v+I}$

jest algebrą Clifforda ${\displaystyle C\ell (V,Q).}$

(1) Liczby zespolone tworzą trywialną algebrę Clifforda ${\displaystyle C\ell _{0,1}(\mathbb {R} ).}$ Mogą zostać skonstruowane w następujący sposób. Niech ${\displaystyle V=\mathbb {R} .}$ Połóżmy ${\displaystyle C:=\mathbb {R} ^{2}.}$ Oznaczamy ${\displaystyle i:=(0,1)}$ i kładziemy ${\displaystyle i^{2}=-1.}$ Przekształcenie liniowe ${\displaystyle j\colon V\to C}$ jest dane wzorem

${\displaystyle j(x)=(0,x)=xi.}$

Mamy

${\displaystyle (j(v))^{2}=(vi)^{2}=-v^{2},}$

a zatem forma ${\displaystyle Q\colon V\to \mathbb {R} }$ jest dana wzorem

${\displaystyle Q(x)=-x^{2}.}$

(2) Kwaterniony są algebrą Clifforda ${\displaystyle C\ell _{0,2}(\mathbb {R} ).}$ Mogą zostać skonstruowane w następujący sposób. Niech ${\displaystyle V=\mathbb {R} ^{2}.}$ Połóżmy ${\displaystyle C:=\mathbb {R} ^{4}.}$

Oznaczmy ${\displaystyle i:=(0,1,0,0),\quad j:=(0,0,1,0),\quad k:=(0,0,0,1)}$ i połóżmy

${\displaystyle i^{2}=j^{2}=k^{2}=ijk=-1.}$

Te związki pozwalają już znaleźć iloczyn każdych dwóch wektorów z ${\displaystyle C.}$

Przekształcenie liniowe ${\displaystyle j\colon V\to C}$ jest dane wzorem

${\displaystyle j(x,y)=(0,x,y,0)=xi+yj.}$

Mamy

${\displaystyle (j(v))^{2}=(j(x,y))^{2}=(xi+yj)^{2}=x^{2}i^{2}+y^{2}j^{2}+xyij+xyji=-x^{2}-y^{2}.}$

Forma kwadratowa ${\displaystyle Q\colon V\to \mathbb {R} }$ jest zatem dana wzorem

${\displaystyle Q(x,y)=-x^{2}-y^{2}.}$

(3) Rozpatrzmy ${\displaystyle 2}$-wymiarową podprzestrzeń ${\displaystyle \mathrm {Mat} _{2\times 2}(\mathbb {R} )}$ złożoną z macierzy postaci ${\displaystyle {\begin{pmatrix}a&b\\b&-a\end{pmatrix}}.}$ Nazwijmy ją ${\displaystyle V.}$ Jej bazę stanowią macierze ${\displaystyle e_{1}:={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}}$ i ${\displaystyle e_{2}:={\begin{pmatrix}0&1\\1&0\end{pmatrix}}.}$ Mamy

${\displaystyle e_{3}:={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}{\begin{pmatrix}0&1\\1&0\end{pmatrix}}={\begin{pmatrix}0&1\\-1&0\end{pmatrix}}.}$

Za ${\displaystyle C}$ przyjmujemy algebrę rozpiętą przez ${\displaystyle e_{1},e_{2},e_{3}}$ i macierz jednostkową ${\displaystyle e_{0}=\mathrm {1} }$ ze zwykłym mnożeniem macierzowym. Mamy

${\displaystyle {\begin{pmatrix}a&b\\b&-a\end{pmatrix}}{\begin{pmatrix}a&b\\b&-a\end{pmatrix}}=(a^{2}+b^{2}){\begin{pmatrix}1&0\\0&1\end{pmatrix}},}$

a zatem ${\displaystyle C}$ wraz z ${\displaystyle j:=\mathrm {id} _{V},}$ jest algebrą Clifforda formy kwadratowej ${\displaystyle Q\colon V\to \mathbb {R} }$ danej wzorem

${\displaystyle Q(v)=Q\left({\begin{pmatrix}a&b\\b&-a\end{pmatrix}}\right)=a^{2}+b^{2}.}$

(4)

• Liczby podwójne to algebra Clifforda ${\displaystyle C\ell _{1,0}(\mathbb {R} ).}$
• Kokwaterniony to algebra Clifforda ${\displaystyle C\ell _{1,1}(\mathbb {R} )}$ albo ${\displaystyle C\ell _{2,0}(\mathbb {R} ).}$
• Bikwaterniony to algebra Clifforda ${\displaystyle C\ell _{0,3}(\mathbb {R} ).}$
• Liczby dualne to algebra Clifforda zdegenerowanej formy ${\displaystyle Q}$ tzn. równej tożsamościowo zero.

• algebra tensorowa
• algebra zewnętrzna
• iloczyn tensorowy przestrzeni liniowych

• J. Komorowski: Od liczb zespolonych do tensorów, spinorów, algebr Liego i kwadryk. Warszawa: Państwowe Wydawnictwo Naukowe, 1978.

• Wybrane zagadnienia algebry
• Clifford algebra (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2024-04-05].