Graf Petersena
Graf Petersena – w teorii grafów, szczególny graf kubiczny o 10 wierzchołkach i 15 krawędziach[1]. Nazwany na cześć matematyka Juliusa Petersena, który w 1898 podał go jako przykład grafu regularnego stopnia 3 bez mostów, którego krawędzi nie można pokolorować trzema kolorami[2][3].
Graf Petersena
Graf Petersena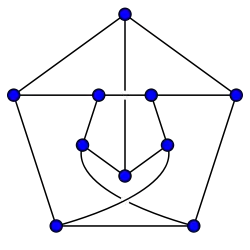 narysowany z dwoma przecięciami.
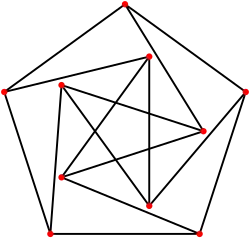Graf Petersena narysowany tak, że wszystkie krawędzie są tej samej długości.
Własności
Graf Petersena...
- jest silnie regularny stopnia 3.
- jest trójspójny i trójspójny krawędziowo.
- ma ścieżkę Hamiltona, ale nie ma cyklu Hamiltona.
- jest grafem trójdzielnym.
- jest dopełnieniem grafu krawędziowego grafu K5.
- jest symetryczny, to znaczy krawędziowo tranzytywny i wierzchołkowo tranzytywny.
- nie jest grafem planarnym.
Własności grafu Petersena:
| liczba wierzchołków | 10 |
|---|---|
| liczba krawędzi | 15 |
| Stopień | 3 |
| liczba chromatyczna | 3 |
| indeks chromatyczny | 4 |
| promień | 2 |
| średnica | 2 |
| obwód | 5 |
| widmo | −2, −2, −2, −2, 1, 1, 1, 1, 1, 3 |
Inne cechy
- jest najmniejszym żmirłaczem.
- jest najmniejszym grafem kubicznym bez mostów i cykli Hamiltona.
- jest największym grafem kubicznym o średnicy 2.
- jest najmniejszym grafem hipohamiltonowskim.
Przypisy
- ↑ Eric W. Weisstein, Petersen Graph [online], Wolfram MathWorld [dostęp 2024-04-28] (ang.).
- ↑ Andries Brouwer, The Petersen graph [online] [dostęp 2024-04-28] (ang.).
- ↑ Julius Petersen, Sur le théorème de Tait, „L'Intermédiaire des mathématiciens”, 1898, s. 225-227 [dostęp 2024-04-28] (fr.).
Linki zewnętrzne
Eric W. Weisstein, Petersen Graph, [w:] MathWorld, Wolfram Research [dostęp 2024-04-28] (ang.).
| pojęcia podstawowe | |
|---|---|
| problemy grafowe | |
| algorytmy grafowe | |
| inne zagadnienia |
