Algorytm Edmondsa-Karpa
| Rodzaj | |
|---|---|
| Struktura danych | |
| Złożoność | |
| Czasowa |
O(VE²) |
Algorytm Edmondsa-Karpa jest jedną z realizacji metody Forda-Fulkersona rozwiązywania problemu maksymalnego przepływu w sieci przepływowej. Jego złożoność czasowa wynosi jest zatem wolniejszy od innych znanych algorytmów przepływowych działających w czasie takich jak algorytm relabel-to-front, czy algorytm trzech Hindusów. W praktyce jednak złożoność pesymistyczna rzadko jest osiągana, co w połączeniu z prostotą czyni algorytm Edmondsa-Karpa bardzo użytecznym, szczególnie dla grafów rzadkich.
Algorytm ten został odkryty przez rosyjskiego naukowca, E.A. Dinica w roku 1970[1], i niezależnie przez Jacka Edmondsa i Richarda Karpa w roku 1972[2]. Artykuł Dinica zawiera dodatkowe techniki, które obniżają czas działania do (algorytm z tą poprawką nazywa się obecnie algorytmem Dynica).
Algorytm
Idea algorytmu jest identyczna z ideą metody Forda-Fulkersona, z dodatkowym warunkiem: ścieżka powiększająca, którą szukamy w każdym kroku algorytmu, musi być najkrótsza, czyli zawierać minimalną możliwą liczbę (nie wagę!) krawędzi. Taką ścieżkę znajduje się uruchamiając algorytm przeszukiwania grafu wszerz w sieci residualnej.
algorytm Edmonds-Karp
wejście
c[u,v] //pojemności krawędzi
s,t //źródło i ujście
wyjście
f[u,v] //maksymalny przepływ
// stworzenie sieci residualnej
zdefiniuj r[u,v] jako c[u,v] – f[u,v]
ścieżka := true
dopóki ścieżka wykonaj
// znalezienie ścieżki z s do t w sieci residualnej
p := BFS(r[],s,t)
jeżeli ścieżka nie istnieje
ścieżka := false
w przeciwnym wypadku
// powiększenie przepływu na ścieżce p
a := min {r[u,v] : (u,v) należące do p}
dla każdej krawędzi (u,v) należącej do p
f[u,v] = f[u,v]+a
f[v,u] = f[v,u]-a
Poprawność i złożoność
Poprawność algorytmu wynika wprost z twierdzenia Forda-Fulkersona: po zakończeniu działania w grafie nie może być ścieżki powiększającej, przepływ jest więc maksymalny. Przystępny dowód oszacowania złożoności czasowej można znaleźć w[3], opiera się on na fakcie, że długość ścieżki powiększającej nie może maleć, a utrzymywać się na tym samym poziomie może przez co najwyżej kroków algorytmu (czyli jest co najwyżej kroków, jako że długość ścieżki nie przekroczy ).
Przykład
Dana jest następująca sieć przepływowa:

Wierzchołek A jest źródłem, G ujściem. Pary liczb na krawędziach oznaczają odpowiednio bieżący przepływ i maksymalną pojemność krawędzi. Pojemność residualna krawędzi z do to pojemność maksymalna zmniejszona o aktualny przepływ. Należy zwrócić uwagę na to, że f[u,v] może być ujemne, co powiększa pojemność krawędzi.
| Opis | Znaleziona ścieżka |
|---|---|
| Sieć po powiększeniu | |
| Najkrótsza powiększająca ścieżka ma długość 3 i składa się z krawędzi AD (pojemność residualna 3-0 = 3), DE (2-0 = 2), i EG (1-0 = 1). Minimalna pojemność residualna to 1, powiększamy zatem przepływ na tej ścieżce o 1. | |
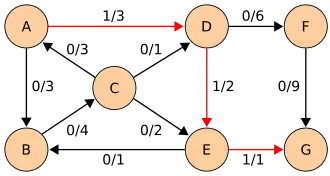 | |
| Najkrótsza ścieżka: AD (3-1 = 2), DF (6-0 = 6), FG (9-0 = 9).
Minimalna pojemność residualna: 2. |
|
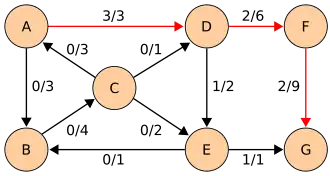 | |
| Najkrótsza ścieżka: AB (3-0 = 3), BC (4-0 = 4), CD (1-0 = 1), DF (6-2 = 4), FG (7-2 = 5).
Minimalna pojemność residualna: 1. |
|
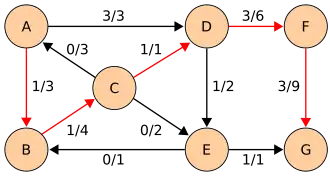 | |
| Najkrótsza ścieżka: AB (3-1 = 2), BC (4-1 = 3), CE (2-0 = 2), ED (0-(-1) = 1), DF (6-3 = 3), FG (9-3 = 6).
Minimalna pojemność residualna: 1. Krawędź ED nie występuje w oryginalnym grafie (jej pojemność to 0), jest jednak obecna w sieci residualnej – przepływ na niej wynosi -1, gdyż przepływ na DE wynosi 1. Stąd pojemność residualna ED jest równa 1 i możemy tej krawędzi użyć w ścieżce powiększającej. |
|
 |
W powstałej sieci nie ma już ścieżek powiększających, zatem znaleziony przepływ o wielkości 5 jest maksymalny. Przykład dobrze ilustruje podstawową własność algorytmu Edmondsa-Karpa: długości ścieżek powiększających w kolejnych krokach nie mogą maleć.
Zobacz też
Przypisy
- ↑ E.A. Dinic, Algorithm for solution of a problem of maximum flow in a network with power estimation, Советский мат, том 11, Доклады 1970.
- ↑ Jack Edmonds, Richard Karp. Theoretical improvements in algorithmic efficiency for network flow problems. „Journal of the ACM”. 19/1972. s. 248-264.
- ↑ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford Wprowadzenie do algorytmów, wyd. 7, WNT 2007, ISBN 83-204-3149-2.
