Polilogarytm
Polilogarytm (funkcja Jonquière’a) – funkcja specjalna zdefiniowana w następujący sposób:
- [1].
Szereg ten jest zbieżny dla i dowolnego zespolonego Z tego względu to punkt osobliwy dla każdego
Można także zdefiniować polilogarytm w sposób rekurencyjny:
dla
Uogólnieniem funkcji jest funkcja przestępna Lercha (ang. Lerch transcendent)[1][2].
Wykresy na płaszczyźnie zespolonej


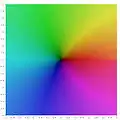
Wykresy funkcji zespolonej uzyskane techniką kolorowania dziedziny
Niektóre własności[1]
- Redukcja do funkcji ζ Riemanna:
- Redukcja do funkcji η Dirichleta:
- Relacje z funkcja przestępną Lercha (ang. Lerch transcendent)[2]:
Przypisy
- 1 2 3 Eric W. Weisstein, Polylogarithm, [w:] MathWorld, Wolfram Research [dostęp 2018-01-01] (ang.).
- 1 2 Eric W. Weisstein, Lerch Transcendent, [w:] MathWorld, Wolfram Research [dostęp 2018-01-01] (ang.).
