Prawa De Morgana

Prawa De Morgana – zestaw reguł w logice matematycznej i teorii mnogości, konkretniej w klasycznym rachunku zdań, rachunku kwantyfikatorów i algebry zbiorów. Prawa De Morgana wiążą ze sobą pary spójników, kwantyfikatorów lub działań na zbiorach za pomocą negacji lub funkcji dopełnienia zbioru^[1]. Prawa te są twierdzeniami w niektórych teoriach formalnych, np. w logice klasycznej, lub aksjomatami definiującymi niektóre struktury jak algebry De Morgana.

Prawa te sformułował Augustus De Morgan – angielski matematyk z XIX wieku.

I prawo De Morgana – zaprzeczania koniunkcji

negacja koniunkcji jest równoważna alternatywie negacji

${\displaystyle \lnot (p\land q)\iff (\lnot p\lor \lnot q),}$

gdzie ${\displaystyle p}$ i ${\displaystyle q}$ oznaczają zdania w sensie logiki.

II prawo De Morgana – zaprzeczenia alternatywy

negacja alternatywy jest równoważna koniunkcji negacji

${\displaystyle \lnot (p\lor q)\iff (\lnot p\land \lnot q).}$

Prawa umożliwiają definiowanie jednych spójników zdaniowych za pomocą innych. Na przykład korzystając z koniunkcji i negacji, za pomocą prawa podwójnej negacji można określić alternatywę:

${\displaystyle p\lor q\iff \lnot (\lnot p\land \lnot q).}$

Do praw De Morgana należą też reguły zaprzeczania kwantyfikatorom^[2][1]:

${\displaystyle \lnot {\bigg (}\forall _{x}\ p(x){\bigg )}\iff {\bigg (}\exists _{x}\ \lnot p(x){\bigg )},}$

${\displaystyle \lnot {\bigg (}\exists _{x}\ p(x){\bigg )}\iff {\bigg (}\forall _{x}\ \lnot p(x){\bigg )},}$

gdzie ${\displaystyle p(x)}$ jest dowolnym zdaniem zależnym od zmiennej ${\displaystyle x.}$

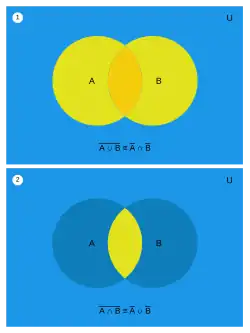
W teorii mnogości prawa De Morgana służą opisowi działania dopełnienia^[1] lub szerzej różnicy zbiorów:

1. dopełnienie sumy zbiorów jest równe części wspólnej ich dopełnień

   ${\displaystyle (A\cup B)^{c}=A^{c}\cap B^{c},}$

2. dopełnienie części wspólnej zbiorów jest równe sumie ich dopełnień

   ${\displaystyle (A\cap B)^{c}=A^{c}\cup B^{c}.}$

Z zasady indukcji matematycznej to samo prawo zachowane jest dla skończenie wielu zdarzeń:

${\displaystyle \left(\bigcup _{i\in I}~A_{i}\right)^{c}=\bigcap _{i\in I}~A_{i}^{c},}$

${\displaystyle \left(\bigcap _{i\in I}~A_{i}\right)^{c}=\bigcup _{i\in I}~A_{i}^{c},}$

gdzie ${\displaystyle I\subset \mathbb {N} .}$

Analogicznie wysławia się i zapisuje prawa De Morgana dla nieskończonych rodzin zbiorów. Wtedy w powyższych wzorach należy przyjąć, że ${\displaystyle I}$ jest taką rodziną.

Jeżeli ${\displaystyle (B,\cup ,\cap ,-,0,1)}$ jest zupełną algebrą Boole’a, to dla ${\displaystyle a_{i}\in B,\,i\in I{:}}$

${\displaystyle -\left(\bigcup _{i\in I}~a_{i}\right)=\bigcap _{i\in I}~-a_{i},}$

${\displaystyle -\left(\bigcap _{i\in I}~a_{i}\right)=\bigcup _{i\in I}~-a_{i}.}$

• K. Kuratowski, A. Mostowski: Teoria mnogości. Wyd. 2. PWN, 1966. Brak numerów stron w książce
• K. Kuratowski: Wstęp do teorii mnogości i topologii. Wyd. 7. PWN, 1977. Brak numerów stron w książce
• H. Rasiowa: Wstęp do matematyki współczesnej. Wyd. 3. PWN, 1971. Brak numerów stron w książce

• Eric W.E.W. Weisstein Eric W.E.W., de Morgan’s Laws, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2023-06-18].
• De Morgan laws (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-06-18].