Problem trzech ciał

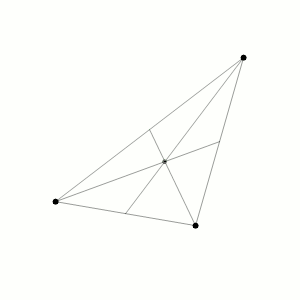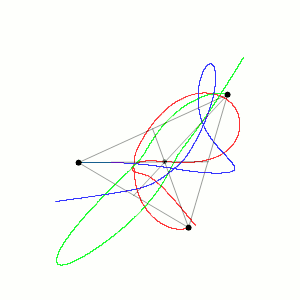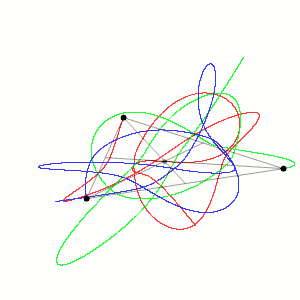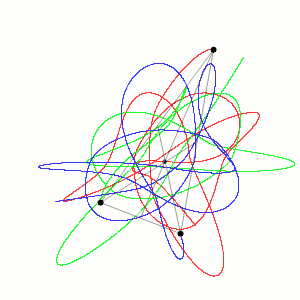
Przybliżone trajektorie trzech identycznych ciał znajdujących się w wierzchołkach trójkąta różnobocznego i mających zerowe prędkości początkowe. Środek masy, zgodnie z zasadą zachowania pędu, pozostaje w tym samym miejscu.

W fizyce, a szczególnie w mechanice klasycznej, problem trzech ciał polega na wyznaczeniu trajektorii trzech punktowych mas poruszających się pod wpływem wzajemnego przyciągania grawitacyjnego. Znając ich początkowe położenia i prędkości (lub pędy), oblicza się ich dalszy ruch za pomocą praw Newtona. ^[1]

W przeciwieństwie do problemu dwóch ciał, problem trzech ciał nie posiada ogólnego rozwiązania w postaci analitycznej, tzn. nie istnieje jedno równanie, które pozwalałoby zawsze wyznaczyć trajektorie. Układ trzech ciał jest w większości przypadków chaotyczny, co oznacza, że nawet niewielkie różnice w początkowych warunkach prowadzą do zupełnie różnych wyników. W praktyce jedynym sposobem przewidzenia ich ruchu jest zastosowanie metod numerycznych.

Problem trzech ciał stanowi szczególny przypadek ogólniejszego problemu n ciał. Historycznie pierwszym dokładnie badanym przypadkiem był układ Ziemia, Księżyc i Słońce.

W szerszym, nowoczesnym ujęciu, problem trzech ciał oznacza dowolny problem w mechanice klasycznej lub kwantowej, w którym analizuje się ruch trzech wzajemnie oddziałujących cząstek.

Opis matematyczny

Matematyczne sformułowanie problemu trzech ciał można przedstawić za pomocą równań ruchu Newtona dla wektorowych położeń $\ \mathbf {r} _{i}=(x_{i},y_{i},z_{i})\$ trzech ciał oddziałujących grawitacyjnie o masach $m_{i}$ :

{\begin{aligned}{\ddot {\mathbf {r} }}_{1}&=-Gm_{2}{\frac {\left(\mathbf {r} _{1}-\mathbf {r} _{2}\right)}{\ \left|\mathbf {r} _{1}-\mathbf {r} _{2}\right|^{3}}}-Gm_{3}{\frac {\left(\mathbf {r} _{1}-\mathbf {r} _{3}\right)}{\ \left|\mathbf {r} _{1}-\mathbf {r} _{3}\right|^{3}}}\ ,\\{\ddot {\mathbf {r} }}_{2}&=-Gm_{3}{\frac {\left(\mathbf {r} _{2}-\mathbf {r} _{3}\right)}{\ \left|\mathbf {r} _{2}-\mathbf {r} _{3}\right|^{3}}}-Gm_{1}{\frac {\left(\mathbf {r} _{2}-\mathbf {r} _{1}\right)}{\ \left|\mathbf {r} _{2}-\mathbf {r} _{1}\right|^{3}}}\ ,\\{\ddot {\mathbf {r} }}_{3}&=-Gm_{1}{\frac {\left(\mathbf {r} _{3}-\mathbf {r} _{1}\right)}{\ \left|\mathbf {r} _{3}-\mathbf {r} _{1}\right|^{3}}}-Gm_{2}{\frac {\left(\mathbf {r} _{3}-\mathbf {r} _{2}\right)}{\ \left|\mathbf {r} _{3}-\mathbf {r} _{2}\right|^{3}}}~.\end{aligned}}

gdzie $G$ to stała grawitacyjna.

Jak opisuje astronom Juhan Frank: „Te trzy wektorowe równania różniczkowe drugiego rzędu są równoważne 18 skalarnym równaniom różniczkowym pierwszego rzędu.”^[2]

Problem można również sformułować w formalizmie Hamiltona, gdzie opisuje się go za pomocą zestawu 18 równań różniczkowych pierwszego rzędu — po jednym dla każdej składowej położeń $\ \mathbf {r} _{i}\$ i pędów $\ \mathbf {p} _{i}\$ :

{\frac {\mathrm {d} \ \mathbf {r} _{i}}{\mathrm {d} \ t}}={\frac {\partial \ {\mathcal {H}}}{\partial \ \mathbf {p} _{i}}}\ ,\qquad {\frac {\mathrm {d} \ \mathbf {p} _{i}}{\mathrm {d} \ t}}=-{\frac {\partial \ {\mathcal {H}}}{\partial \ \mathbf {r} _{i}}}\ ,

gdzie ${\mathcal {H}}$ to Hamiltonian (całkowita energia układu= potencjalna + kinetyczna):

{\mathcal {H}}\ =\ -{\frac {Gm_{1}m_{2}}{\left|\mathbf {r} _{1}-\mathbf {r} _{2}\right|}}\ -\ {\frac {Gm_{2}m_{3}}{\left|\mathbf {r} _{3}-\mathbf {r} _{2}\right|}}\ -\ {\frac {Gm_{3}m_{1}}{\left|\mathbf {r} _{3}-\mathbf {r} _{1}\right|}}\ +\ {\frac {\left|\mathbf {p} _{1}\right|^{2}}{2m_{1}}}\ +\ {\frac {\left|\mathbf {p} _{2}\right|^{2}}{2m_{2}}}\ +\ {\frac {\left|\mathbf {p} _{3}\right|^{2}}{2m_{3}}}~.

Ograniczony problem trzech ciał

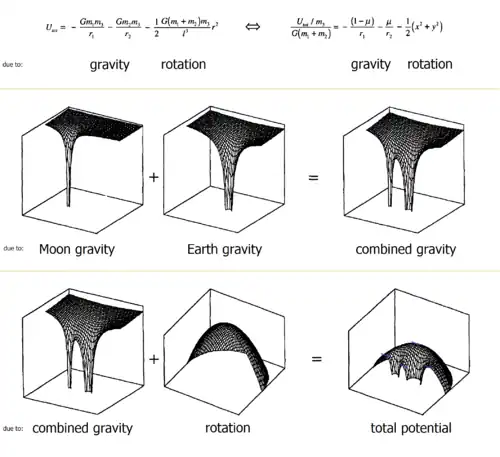
Ograniczony cyrkulacyjny problem trzech ciał jest dobrym przybliżeniem orbit eliptycznych spotykanych w Układzie Słonecznym. Można go zobrazować jako kombinację potencjałów grawitacyjnych dwóch ciał głównych oraz efektu odśrodkowego wynikającego z ich obrotu. Punkty Lagrange’a to miejsca, w których gradient wynikowej powierzchni potencjału wynosi zero, co oznacza równowagę sił.

W wersji „ograniczonego problemu trzech ciał”, jak opisuje Barrow-Green^[3],

dwa ciała... krążą wokół swojego wspólnego środka masy po orbitach kołowych, pod wpływem wzajemnego przyciągania grawitacyjnego i tworzą układ dwóch ciał... [którego] ruch jest znany. Trzecie ciało (zwykle nazywane planetoidą), zakłada się, że ma pomijalną masę względem pozostałych dwóch, porusza się w tej samej płaszczyźnie i choć podlega ich przyciąganiu, samo nie wpływa na ich ruch.

Problem polega zatem na określeniu ruchu tego trzeciego ciała.

Zakłada się, że dwa główne ciała poruszają się po orbitach kołowych wokół wspólnego środka masy, a planetoida porusza się w tej samej płaszczyźnie. W układzie obracającym się względem tych dwóch ciał (tzn. w układzie współrzędnych, w którym oba ciała są nieruchome), trzecie ciało również może pozostawać nieruchome w jednym z punktów Lagrange’a, lub poruszać się wokół nich, np. po orbicie podkowiastej.

Ograniczony problem trzech ciał jest teoretycznie prostszy do analizy niż pełny problem i ma istotne znaczenie praktyczne — dobrze opisuje wiele realnych układów, np. Ziemia–Księżyc–Słońce. Z tego względu odegrał kluczową rolę w historii rozwoju badań nad problemem trzech ciał.^[4]

Problem można przedstawić matematycznie w sposób następujący: Niech $m_{1},m_{2}$ będą masami dwóch ciał głównych, o współrzędnych $(x_{1},y_{1})$ oraz $(x_{2},y_{2})$ . Planetoida ma współrzędne $(x,y)$ . Wybierając jednostki tak, by odległość między ciałami głównymi oraz stała grawitacyjna były równe 1, ruch planetoidy opisują równania:

{\begin{aligned}{\frac {\mathrm {d} ^{2}x}{\mathrm {d} \ t^{2}}}=-m_{1}{\frac {(x-x_{1})}{r_{1}^{3}}}-m_{2}{\frac {(x-x_{2})}{r_{2}^{3}}}\ ,\\{\frac {\mathrm {d} ^{2}y}{\mathrm {d} \ t^{2}}}=-m_{1}{\frac {(y-y_{1})}{r_{1}^{3}}}-m_{2}{\frac {(y-y_{2})}{r_{2}^{3}}}\ ,\end{aligned}}

gdzie $r_{i}={\sqrt {(x-x_{i})^{2}+(y-y_{i})^{2}}},i=1,2$ - promienie wodzące ciał głównych.

Jeśli jednak dwa ciała główne poruszają się po orbitach kołowych ze stałymi prędkościami, to można przejść do układu obracającego się wraz z nimi, co eliminuje zależność czasową z równań i upraszcza dalszą analizę.

Rozwiązania

Ogólne rozwiązanie

Układ trzech ciał oddziałujących grawitacyjnie jest chaotyczny, ale układ trzech ciał oddziałujących sprężyście już niekoniecznie.

Nie istnieje ogólne rozwiązanie w postaci analitycznej problemu trzech ciał.^[1] To znaczy, nie da się przedstawić wzorów, opisujących położenia każdego z trzech ciał układu za pomocą skończonej liczby standardowych operacji matematycznych. Jak wynika z rozwiązań numerycznych, ruch trzech ciał jest na ogół nieregularny i niepowtarzalny – z wyjątkiem szczególnych przypadków^[5].

W 1912 roku fiński matematyk Karl Fritiof Sundman udowodnił, że istnieje rozwiązanie analityczne tego problemu w postaci szeregów Puiseux, a konkretnie szeregów potęgowych względem $t^{1/3}$ ^[6].

Szereg ten jest zbieżny dla wszystkich liczb rzeczywistych $t$ z wyjątkiem przypadków, gdy całkowity moment pędu $L$ układu wynosi zero, $L=0$ . W praktyce przypadki takie są niezwykle rzadkie i mają miarę Lebesgue’a równą zeru.

Istotnym aspektem tego rozwiązania jest to, że promień zbieżności szeregu zależy od odległości do najbliższej osobliwości. Sundman wykazał, że jedynymi osobliwościami są kolizje: podwójne lub potrójne. Kolizje trzech ciał są możliwe tylko wtedy, gdy moment pędu wynosi zero. Dlatego:

Wprowadził transformację zmiennych (tzw. regularyzację) umożliwiającą kontynuowanie rozwiązania pomijające kolizje dwóch ciał w układzie.
Ograniczył zbiór danych początkowych do przypadków z $L\neq 0$ , co wykluczyło rzeczywiste osobliwości.
Wykazał, że dla $L\neq 0$ układ nie może zbliżyć się do kolizji potrójnej.
Zastosował odwzorowanie konforemne zamieniające pasmo zespolone wokół osi rzeczywistej na koło jednostkowe, np. przez podstawienie:

$\sigma ={\frac {e^{\frac {\pi s}{2\beta }}-1}{e^{\frac {\pi s}{2\beta }}+1}},\quad {\text{gdzie }}s=t^{1/3}.$

To kończy dowód twierdzenia Sundmana.

Praktyczne zastosowanie tego rozwiązania jest jednak bardzo ograniczone – szereg zbiega niezwykle wolno. W 1930 roku David Beloriszky oszacował, że do uzyskania dokładności potrzebnej w astronomii potrzeba byłoby około 10^{8 000 000} wyrazów^[7].

Rozwiązania szczególne

Animacja rozwiązania typu „ósemka” w problemie trzech ciał; okres obiegu T ≃ 6,3259^[8]

20 przykładów okresowych rozwiązań problemu trzech ciał. (Kliknij w obrazek, by zobaczyć animacje ruchu ciał)

W 1767 roku Leonhard Euler odkrył trzy rodziny rozwiązań okresowych, w których trzy masy są zawsze ustawione wzdłuż jednej linii.

W 1772 roku Lagrange znalazł rodzinę rozwiązań, w których masy tworzą trójkąt równoboczny w każdej chwili. Razem z rozwiązaniami Eulera tworzą one tzw. konfiguracje centralne dla problemu trzech ciał. Są one poprawne dla dowolnych proporcji mas, a ciała poruszają się po orbitach Keplerowskich. W szczególnym przypadku ograniczonego cyrkulacyjnego problemu trzech ciał, te rozwiązania stają się punktami stacjonarnymi w układzie obrotowym – są to punkty Lagrange’a L₁–L₅.

W latach 1892–1899 Henri Poincaré udowodnił istnienie nieskończonej liczby rozwiązań okresowych ograniczonego problemu trzech ciał i opracował metody ich kontynuowania w ogólnym przypadku.

W 1893 roku Meissel sformułował tzw. „pitagorejski problem trzech ciał”: trzy masy o stosunku 3:4:5 rozmieszczone w wierzchołkach trójkąta prostokątnego i pozostające w spoczynku. W 1913 roku problem ten szczegółowo badał Burrau^[9], a w 1967 Szebehely i Peters wykazali, że najlżejsze ciało ostatecznie ucieka z układu.

W latach 70. XX w. Michel Hénon i Roger A. Broucke odkryli rodzinę rozwiązań, w których trzy jednakowe masy poruszają się w układzie okresowym – niektóre z tych rozwiązań mają trajektorie, w których dwa ciała podążają tą samą ścieżką^[10].

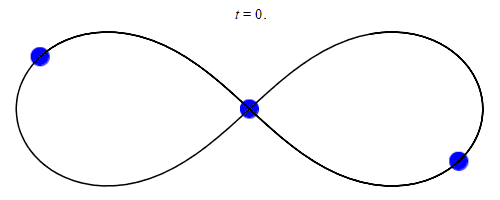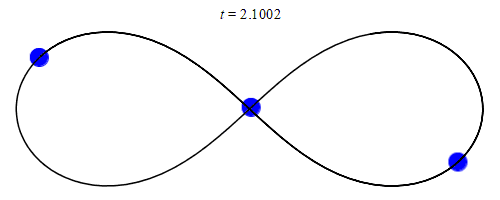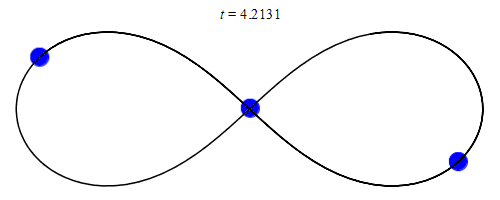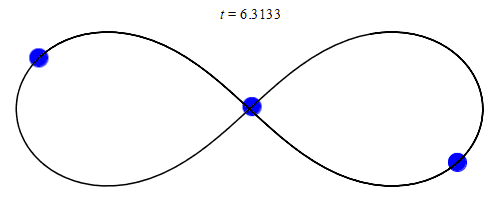
W 1993 roku Cris Moore z Instytutu Santa Fe odkrył rozwiązanie z zerowym momentem pędu, w którym trzy jednakowe masy poruszają się po trajektorii w kształcie „ósemki”^[11]. W 2000 roku Alain Chenciner i Richard Montgomery formalnie dowiedli istnienia tego rozwiązania^[12].

W 2013 roku Milovan Šuvakov i Veljko Dmitrašinović odkryli 13 nowych rodzin rozwiązań dla problemu trzech ciał z równymi masami i zerowym momentem pędu^[5]^[10].

W 2015 roku fizyczka Ana Hudomal odkryła 14 kolejnych rodzin takich rozwiązań^[13].

W 2017 Xiaoming Li i Shijun Liao znaleźli 669 nowych okresowych orbit, a w 2018 kolejne 1223 rozwiązania dla układów z nierównymi masami^[14].

W 2023 roku Ivan Hristov, Radoslava Hristova, Veljko Dmitrašinović i Kiyotaka Tanikawa opublikowali 12 409 rozwiązań dla tzw. „okresowych orbit swobodnego spadku” w przypadku równych mas.^[15]

Podejścia numeryczne

Przy użyciu komputera problem może być rozwiązany z dowolnie wysoką precyzją za pomocą całkowania numerycznego. Podejmowano próby tworzenia programów komputerowych, które numerycznie rozwiązują problem trzech ciał (a w szerszym ujęciu problem n ciał), uwzględniających zarówno oddziaływania elektromagnetyczne jak i grawitacyjne oraz włączających współczesne teorie fizyczne, takie jak szczególna teoria względności^[16]. Dodatkowo, przy użyciu teorii błądzenia losowego, można obliczyć przybliżone prawdopodobieństwo różnych wyników^[17]^[18].

Historia

Problem grawitacyjny trzech ciał w swoim tradycyjnym sensie datuje się zasadniczo od roku 1687, kiedy Izaak Newton opublikował dzieło Philosophiæ Naturalis Principia Mathematica, w którym próbował ustalić, czy możliwa jest jakakolwiek długoterminowa stabilność w układzie takim jak Ziemia, Księżyc i Słońce, po wcześniejszym rozwiązaniu problem dwóch ciał.^[19] Kierując się osiągnięciami wielkich astronomów renesansu: Mikołaja Kopernika, Tycho Brah i Johannesa Keplera, Newton zapoczątkował badania nad problemem trzech ciał grawitacyjnych^[20]. W Propozycji 66 Księgi I Principiów i jej 22 Korolariach Newton postawił pierwsze kroki w definiowaniu i badaniu ruchów trzech masywnych ciał podlegających wzajemnym zaburzeniom grawitacyjnym (Propozycja - to twierdzenie, Koloraria - to wnioski, wysnuwane z twierdzeń). W Propozycjach 25–35 Księgi III zastosował te wyniki do teorii Księżyca, analizując ruch Księżyca pod wpływem grawitacji Ziemi i Słońca^[21]. Później problem ten zastosowano również do oddziaływań innych planet z Ziemią i Słońcem^[20].

Problem fizyczny był wcześniej rozważany przez Amerigo Vespucciego, następnie przez Galileusza i Simona Stevina, lecz nie zdawali sobie oni sprawy z wagi swoich wkładów. Galileusz, choć wykazał, że prędkość spadania wszystkich ciał zmienia się jednakowo, nie zastosował tej wiedzy do ruchów planet^[20]. Tymczasem już w 1499 roku Vespucci użył pozycji Księżyca do określenia swojego położenia w Brazylii^[22]. W latach 20. XVIII wieku problem ten nabrał znaczenia technicznego, gdyż jego dokładne rozwiązanie mogło pomóc w wyznaczaniu długości geograficznej na morzu, co w praktyce udało się dzięki Johnowi Harrisonowi i jego chronometrowi morskiemu. Jednak dokładność teorii Księżyca była niska, ze względu na zakłócenia spowodowane wpływem Słońca i planet.

Jean le Rond d'Alembert i Alexis Clairaut, którzy rywalizowali ze sobą przez wiele lat, podjęli próbę ogólnej analizy tego problemu i przedstawili swoje konkurencyjne opracowania w Akademii Nauk w Paryżu w 1747 roku^[23]. Właśnie w związku z tymi badaniami, prowadzonymi w Paryżu w latach 40. XVIII w., zaczęto powszechnie używać nazwy „problem trzech ciał”. D’Alembert w opisie z 1761 roku wskazywał, że nazwa ta została po raz pierwszy użyta w 1747 roku^[24].

Od końca XIX do początku XX wieku rozwijano podejście do problemu trzech ciał z użyciem metody krótkozasięgowych sił przyciągania między parami ciał. To podejście umożliwiło P. F. Bedaque, H.-W. Hammerowi i U. van Kolckowi sformułowanie pomysłu renormalizacji tego problemu, dając rzadki przykład cyklu granicznego już na początku XXI wieku^[25]. George William Hill pracował nad wersją ograniczoną problemu pod koniec XIX wieku, analizując ruch Wenus i Merkurego^[26].

Na początku XX wieku Karl Sundman podszedł do problemu matematycznie i systematycznie, dostarczając funkcjonalnego dowodu teoretycznego ważnego dla wszystkich wartości czasu. Było to pierwsze teoretyczne rozwiązanie problemu trzech ciał. Jednak rozwiązanie to było zbyt wolne i nie miało wystarczającej jakości, by znaleźć praktyczne zastosowanie^[27]. W latach 70. XX wieku Witalij Efimow odkrył, że krótkozasięgowe siły dwuciałowe mogą prowadzić do efektów trójciałowych, co nazwano efektem Efimowa^[28].

W 2017 roku Liao Shijun i Xiaoming Li zastosowali nową strategię symulacji numerycznych dla układów chaotycznych, tzw. „czystą symulację numeryczną” (CNS), wykorzystując superkomputer krajowy, uzyskując 695 rodzin rozwiązań okresowych dla układu trzech ciał o jednakowych masach^[29].

W 2019 roku Breen i in. ogłosili opracowanie szybkiego programu opartego na sieci neuronowej dla problemu trzech ciał, wytrenowany przy użyciu całkowania numerycznego^[30].

We wrześniu 2023 roku ogłoszono odkrycie 12 tysięcy możliwych rozwiązań tego problemu^[31]^[32].

Problem n ciał

Problem trzech ciał jest szczególnym przypadkiem problemu n ciał, który opisuje, jak n obiektów porusza się pod wpływem jednej z sił fizycznych, takich jak grawitacja. Problemy te mają ogólne rozwiązanie analityczne w postaci zbieżnego szeregu potęgowego, co zostało udowodnione przez Karla F. Sundmana dla $n=2$ oraz przez Qiudong Wanga dla $n=3$ (szczegóły zobacz w haśle problem n ciał). Jednak szeregi Sundmana i Wanga zbieżne są tak wolno, że są bezużyteczne w praktyce^[33]; dlatego obecnie rozwiązania trzeba przybliżać za pomocą analizy numerycznej w postaci całkowania numerycznego lub, w niektórych przypadkach, klasycznych przybliżeń w postaci szeregów trygonometrycznych.

Układy atomowe, np. atomy, jony i cząsteczki, można traktować w kategoriach kwantowego problemu n ciał. Wśród klasycznych układów fizycznych problem n ciał odnosi się zwykle do galaktyki lub gromady galaktyk; układy planetarne, takie jak gwiazdy, planety i ich księżyce, również można traktować jako układy n ciał. Niektóre zastosowania wygodnie opisuje się z teorii zaburzeń, w której układ traktuje się jako problem dwóch ciał z dodatkowymi siłami powodującymi odchylenia od hipotetycznej, niezaburzonej trajektorii dwuciałowej.

Zobacz też

Pokrewne:

Inne:

Przypisy

1 2 June Barrow-Green: The Three-Body Problem. red. Timothy Gowers, June Barrow-Green, Imre Leader. Princeton University Press, 2008, s. 726–728. ISBN 978-0-691-11880-2.
↑ Frank, Juhan (2006). „PHYS 7221 Special Lecture—The Three-Body Problem”, Louisiana State University.
↑ June Barrow-Green: Poincaré and the Three Body Problem. Providence: American Mathematical Society, 1997. ISBN 978-0-8218-0367-7.
↑ RichardR. Montgomery RichardR., The Three-Body Problem, „Scientific American”, 321 (2), 2019, s. 66, DOI: 10.1038/scientificamerican0819-66, PMID: 39010603 [dostęp 2024-05-07] .
1 2 JonJ. Cartwright JonJ., Physicists Discover a Whopping 13 New Solutions to Three-Body Problem, „Science Now”, 8 marca 2013 [dostęp 2013-04-04] .
↑ Barrow-Green, June (2010). „The dramatic episode of Sundman”, Historia Mathematica 37, s. 164–203.
↑ D.D. Beloriszky D.D., Application pratique des méthodes de M. Sundman à un cas particulier du problème des trois corps, „Bulletin Astronomique”, 6 (Série 2), 1930, s. 417–434, Bibcode: 1930BuAst...6..417B .
↑ Z wartościami początkowymi: r₁(0) = -r₃(0) = (−0.97000436, 0.24308753); r₂(0) = (0,0); v₁(0) = v₃(0) = (0.4662036850, 0.4323657300); v₂(0) = (−0.93240737, −0.86473146).
↑ Burrau. Numerische Berechnung eines Spezialfalles des Dreikörperproblems. „Astronomische Nachrichten”. 195 (6), s. 113–118, 1913. DOI: 10.1002/asna.19131950602. Bibcode: 1913AN....195..113B.
1 2 Šuvakov, M., Dmitrašinović, V.: Three-body Gallery. [dostęp 2015-08-12].
↑ Moore, Cristopher. Braids in classical dynamics. „Physical Review Letters”. 70 (24), s. 3675–3679, 1993. DOI: 10.1103/PhysRevLett.70.3675. PMID: 10053934.
↑ Chenciner, Alain, Montgomery, Richard. A remarkable periodic solution of the three-body problem in the case of equal masses. „Annals of Mathematics”. 152 (3), s. 881–902, 2000. DOI: 10.2307/2661357.
↑ AnaA. Hudomal AnaA., New periodic solutions to the three-body problem and gravitational waves, „Master of Science Thesis at the Faculty of Physics, Belgrade University”, październik 2015 [dostęp 2019-02-05] (ang.).
↑ XiaomingX. Li XiaomingX., ShijunS. Liao ShijunS., The 1223 new periodic orbits of planar three-body problem with unequal mass and zero angular momentum, „Publications of the Astronomical Society of Japan”, 70 (4), 2018, s. 64, DOI: 10.1093/pasj/psy057 .
↑ Hristov, Ivan, Hristova, Radoslava, Dmitrašinović, Veljko, Tanikawa, Kiyotaka. Three-body periodic collisionless equal-mass free-fall orbits revisited. „Celestial Mechanics and Dynamical Astronomy”. 136 (1), s. 7, 2024. DOI: 10.1007/s10569-023-10177-w.
↑ 3body simulator [online], 3body simulator [dostęp 2022-11-17] [zarchiwizowane z adresu] (ang.).
↑ Technion, A Centuries-Old Physics Mystery? Solved [online], SciTechDaily, 2021 [dostęp 2021-10-12] (ang.).
↑ Yonadav Barry Ginat, Hagai B. Perets. Analytical, Statistical Approximate Solution of Dissipative and Nondissipative Binary-Single Stellar Encounters. „Physical Review X”. 11 (3), s. 031020, 2021-07-23. DOI: 10.1103/PhysRevX.11.031020. arXiv:2011.00010. Bibcode: 2021PhRvX..11c1020G. [dostęp 2021-10-12]. (ang.).
↑ Zdzislaw Musielak, Billy Quarles: Three Body Dynamics and Its Applications to Exoplanets. Springer International Publishing, 2017. ISBN 978-3-319-58225-2.
1 2 3 Mauri Valtonen: The Three-body Problem from Pythagoras to Hawking. Springer, 2016, s. 4. ISBN 978-3-319-22726-9. OCLC 1171227640.
↑ Isaac Newton: Philosophiæ naturalis principia mathematica. Hong Kong University of Science and Technology. London: G. & J. Innys, 1726. DOI: 10.14711/spcol/b706487. [dostęp 2022-10-05].
↑ Amerigo Vespucci, [w:] Biography [online], 23 czerwca 2021 [dostęp 2022-10-05] (ang.).
↑ Obie prace z 1747 roku można przeczytać w tomie Histoires (w tym Mémoires) Akademii Królewskiej Nauk za 1745 (wydanym z opóźnieniem w 1749 roku) (po francusku):
Clairaut: "O systemie świata według zasad powszechnego ciążenia" (s. 329–364);

d'Alembert: "Ogólna metoda wyznaczania orbit i ruchów wszystkich planet, uwzględniająca ich wzajemne oddziaływania" (s. 365–390). Uwaga na s. 390 wyjaśnia datowanie: "Choć powyższe pamiętniki panów Clairauta i d'Alemberta były czytane dopiero w 1747 roku, uznano za właściwe opublikować je w tomie za ten rok" (czyli w tomie poświęconym obradom z 1745 roku, ale wydanym w 1749).
↑ Jean le Rond d'Alembert, w artykule z 1761 roku przeglądającym historię matematyczną problemu, wspomina, że Euler opracował metodę całkowania pewnego równania różniczkowego "w 1740 roku (siedem lat przed tym, jak pojawiła się kwestia problemu trzech ciał)": zob. d'Alembert, "Opuscules Mathématiques", t. 2, Paryż 1761, Quatorzième Mémoire ("Réflexions sur le Problème des trois Corps..."), s. 329–312, sekcja VI, s. 245.
↑ R.F. Mohr, R.J. Furnstahl, H.-W. Hammer, R.J. Perry i inni. Precyzyjne wyniki numeryczne dla cykli granicznych w kwantowym problemie trzech ciał. „Annals of Physics”. 321 (1), s. 225–259, January 2006. DOI: 10.1016/j.aop.2005.10.002. arXiv:nucl-th/0509076. Bibcode: 2006AnPhy.321..225M.
↑ "Ruch dwóch planet w jednej płaszczyźnie, z których jedna ma zerową masę". Annals of Mathematics, t. III, s. 65–73, 1887.
↑ June Barrow-Green: Poincaré and the Three Body Problem. T. 11. Providence, Rhode Island: American Mathematical Society, 1996-10-29, seria: History of Mathematics. DOI: 10.1090/hmath/011. ISBN 978-0-8218-0367-7.
↑ V.V. Efimov V.V., Energy levels arising from resonant two-body forces in a three-body system (Poziomy energetyczne wynikające z rezonansowych sił dwuciałowych w układzie trzech ciał), „Physics Letters B”, 33 (8), 1970, s. 563–564, DOI: 10.1016/0370-2693(70)90349-7, Bibcode: 1970PhLB...33..563E (ang.).
↑ Shijun Liao, Xiaoming Li. O rozwiązaniach okresowych problemu trzech ciał. „National Science Review”. 6 (6), s. 1070–1071, 2019-11-01. DOI: 10.1093/nsr/nwz102. ISSN 2095-5138. PMID: 34691975. PMCID: PMC8291409.
↑ Philip G. Breen, Christopher N. Foley, Tjarda Boekholt, Simon Portegies Zwart. Newton versus the machine: Solving the chaotic three-body problem using deep neural networks (Newton kontra maszyna: Rozwiązywanie chaotycznego problemu trzech ciał za pomocą głębokich sieci neuronowych). „Monthly Notices of the Royal Astronomical Society”. 494 (2), s. 2465–2470, 2020. DOI: 10.1093/mnras/staa713. arXiv:1910.07291.
↑ ClaireC. Watson ClaireC., We Just Got 12,000 New Solutions to The Infamous Three-Body Problem, [w:] ScienceAlert [online], 23 września 2023 [dostęp 2023-09-23] [zarchiwizowane z adresu 2023-09-24] .
↑ Ivan Hristov, Radoslava Hristova, Veljko Dmitrašinović, Kiyotaka Tanikawa. Rewizja okresowych, bezkolizyjnych orbit swobodnego spadku dla trzech ciał o jednakowej masie. „Celestial Mechanics and Dynamical Astronomy”. 136 (1), 2024. DOI: 10.1007/s10569-023-10177-w. arXiv:2308.16159. Bibcode: 2024CeMDA.136....7H.
↑ Florin Diacu. "The Solution of the n-body Problem", The Mathematical Intelligencer, 1996.

Literatura uzupełniająca

S. J. Aarseth: Gravitational n-Body Simulations. Nowy Jork: Cambridge University Press, 2003. ISBN 978-0-521-43272-6.
J. S. Bagla. Cosmological N-body simulation: Techniques, scope and status. „Current Science”. 88, s. 1088–1100, 2005. arXiv:astro-ph/0411043. Bibcode: 2005CSci...88.1088B.
J. E. Chambers, G. W. Wetherill. Making the Terrestrial Planets: N-Body Integrations of Planetary Embryos in Three Dimensions. „Icarus”. 136 (2), s. 304–327, 1998. DOI: 10.1006/icar.1998.6007. Bibcode: 1998Icar..136..304C.
G. Efstathiou, M. Davis, S. D. M. White, C. S. Frenk. Numerical techniques for large cosmological N-body simulations. „Astrophysical Journal”. 57, s. 241–260, 1985. DOI: 10.1086/191003. Bibcode: 1985ApJS...57..241E.
Neal D. Hulkower. The Zero Energy Three Body Problem. „Indiana University Mathematics Journal”. 27 (3), s. 409–447, 1978. DOI: 10.1512/iumj.1978.27.27030. Bibcode: 1978IUMJ...27..409H.
Neal D. Hulkower. Central Configurations and Hyperbolic-Elliptic Motion in the Three-Body Problem. „Celestial Mechanics”. 21 (1), s. 37–41, 1980. DOI: 10.1007/BF01230244. Bibcode: 1980CeMec..21...37H.
Xiaoming Li, Shijun Liao. On the stability of the three classes of Newtonian three-body planar periodic orbits. „Science China Physics, Mechanics & Astronomy”. 57 (11), s. 2121–2126, 2014. DOI: 10.1007/s11433-014-5563-5. arXiv:1312.6796. Bibcode: 2014SCPMA..57.2121L.
Milovan Šuvakov, V. Dmitrašinović. Three Classes of Newtonian Three-Body Planar Periodic Orbits. „Physical Review Letters”. 110 (10), s. 114301, 2013. DOI: 10.1103/PhysRevLett.110.114301. arXiv:1303.0181. PMID: 25166541. Bibcode: 2013PhRvL.110k4301S.

Linki zewnętrzne

W języku polskim:

Zagadnienie trzech ciał - świetna symulacja nieokresowego ruchu trzech ciał prof. dr hab. Adam Bzdak z AGH.
Problem trzech ciał - czy da się rozwiązać? - dyskusja nt. problemu w programie AstroFaza

W języku angielskim:

Problem trzech ciał może nie być aż tak chaotyczny, sugeruje nowe badanie (Live Science, 22 października 2024)
Fizycy odkrywają aż 13 nowych rozwiązań problemu trzech ciał (Science, 8 marca 2013)

[PrincetonCompanion-1] 1 2 June Barrow-Green: The Three-Body Problem. red. Timothy Gowers, June Barrow-Green, Imre Leader. Princeton University Press, 2008, s. 726–728. ISBN 978-0-691-11880-2.

[2] Frank, Juhan (2006). „PHYS 7221 Special Lecture—The Three-Body Problem”, Louisiana State University.

[3] June Barrow-Green: Poincaré and the Three Body Problem. Providence: American Mathematical Society, 1997. ISBN 978-0-8218-0367-7.

[first2024-4] RichardR. Montgomery RichardR., The Three-Body Problem, „Scientific American”, 321 (2), 2019, s. 66, DOI: 10.1038/scientificamerican0819-66, PMID: 39010603 [dostęp 2024-05-07] .

[13solutions-5] 1 2 JonJ. Cartwright JonJ., Physicists Discover a Whopping 13 New Solutions to Three-Body Problem, „Science Now”, 8 marca 2013 [dostęp 2013-04-04] .

[6] Barrow-Green, June (2010). „The dramatic episode of Sundman”, Historia Mathematica 37, s. 164–203.

[7] D.D. Beloriszky D.D., Application pratique des méthodes de M. Sundman à un cas particulier du problème des trois corps, „Bulletin Astronomique”, 6 (Série 2), 1930, s. 417–434, Bibcode: 1930BuAst...6..417B .

[8] Z wartościami początkowymi: r₁(0) = -r₃(0) = (−0.97000436, 0.24308753); r₂(0) = (0,0); v₁(0) = v₃(0) = (0.4662036850, 0.4323657300); v₂(0) = (−0.93240737, −0.86473146).

[Burrau-9] Burrau. Numerische Berechnung eines Spezialfalles des Dreikörperproblems. „Astronomische Nachrichten”. 195 (6), s. 113–118, 1913. DOI: 10.1002/asna.19131950602. Bibcode: 1913AN....195..113B.

[TBG-10] 1 2 Šuvakov, M., Dmitrašinović, V.: Three-body Gallery. [dostęp 2015-08-12].

[11] Moore, Cristopher. Braids in classical dynamics. „Physical Review Letters”. 70 (24), s. 3675–3679, 1993. DOI: 10.1103/PhysRevLett.70.3675. PMID: 10053934.

[12] Chenciner, Alain, Montgomery, Richard. A remarkable periodic solution of the three-body problem in the case of equal masses. „Annals of Mathematics”. 152 (3), s. 881–902, 2000. DOI: 10.2307/2661357.

[13] AnaA. Hudomal AnaA., New periodic solutions to the three-body problem and gravitational waves, „Master of Science Thesis at the Faculty of Physics, Belgrade University”, październik 2015 [dostęp 2019-02-05] (ang.).

[14] XiaomingX. Li XiaomingX., ShijunS. Liao ShijunS., The 1223 new periodic orbits of planar three-body problem with unequal mass and zero angular momentum, „Publications of the Astronomical Society of Japan”, 70 (4), 2018, s. 64, DOI: 10.1093/pasj/psy057 .

[15] Hristov, Ivan, Hristova, Radoslava, Dmitrašinović, Veljko, Tanikawa, Kiyotaka. Three-body periodic collisionless equal-mass free-fall orbits revisited. „Celestial Mechanics and Dynamical Astronomy”. 136 (1), s. 7, 2024. DOI: 10.1007/s10569-023-10177-w.

[16] 3body simulator [online], 3body simulator [dostęp 2022-11-17] [zarchiwizowane z adresu] (ang.).

[17] Technion, A Centuries-Old Physics Mystery? Solved [online], SciTechDaily, 2021 [dostęp 2021-10-12] (ang.).

[18] Yonadav Barry Ginat, Hagai B. Perets. Analytical, Statistical Approximate Solution of Dissipative and Nondissipative Binary-Single Stellar Encounters. „Physical Review X”. 11 (3), s. 031020, 2021-07-23. DOI: 10.1103/PhysRevX.11.031020. arXiv:2011.00010. Bibcode: 2021PhRvX..11c1020G. [dostęp 2021-10-12]. (ang.).

[19] Zdzislaw Musielak, Billy Quarles: Three Body Dynamics and Its Applications to Exoplanets. Springer International Publishing, 2017. ISBN 978-3-319-58225-2.

[:1-20] 1 2 3 Mauri Valtonen: The Three-body Problem from Pythagoras to Hawking. Springer, 2016, s. 4. ISBN 978-3-319-22726-9. OCLC 1171227640.

[21] Isaac Newton: Philosophiæ naturalis principia mathematica. Hong Kong University of Science and Technology. London: G. & J. Innys, 1726. DOI: 10.14711/spcol/b706487. [dostęp 2022-10-05].

[22] Amerigo Vespucci, [w:] Biography [online], 23 czerwca 2021 [dostęp 2022-10-05] (ang.).

[23] Obie prace z 1747 roku można przeczytać w tomie Histoires (w tym Mémoires) Akademii Królewskiej Nauk za 1745 (wydanym z opóźnieniem w 1749 roku) (po francusku):
Clairaut: "O systemie świata według zasad powszechnego ciążenia" (s. 329–364);

d'Alembert: "Ogólna metoda wyznaczania orbit i ruchów wszystkich planet, uwzględniająca ich wzajemne oddziaływania" (s. 365–390). Uwaga na s. 390 wyjaśnia datowanie: "Choć powyższe pamiętniki panów Clairauta i d'Alemberta były czytane dopiero w 1747 roku, uznano za właściwe opublikować je w tomie za ten rok" (czyli w tomie poświęconym obradom z 1745 roku, ale wydanym w 1749).

[24] Jean le Rond d'Alembert, w artykule z 1761 roku przeglądającym historię matematyczną problemu, wspomina, że Euler opracował metodę całkowania pewnego równania różniczkowego "w 1740 roku (siedem lat przed tym, jak pojawiła się kwestia problemu trzech ciał)": zob. d'Alembert, "Opuscules Mathématiques", t. 2, Paryż 1761, Quatorzième Mémoire ("Réflexions sur le Problème des trois Corps..."), s. 329–312, sekcja VI, s. 245.

[:0-25] R.F. Mohr, R.J. Furnstahl, H.-W. Hammer, R.J. Perry i inni. Precyzyjne wyniki numeryczne dla cykli granicznych w kwantowym problemie trzech ciał. „Annals of Physics”. 321 (1), s. 225–259, January 2006. DOI: 10.1016/j.aop.2005.10.002. arXiv:nucl-th/0509076. Bibcode: 2006AnPhy.321..225M.

[26] "Ruch dwóch planet w jednej płaszczyźnie, z których jedna ma zerową masę". Annals of Mathematics, t. III, s. 65–73, 1887.

[27] June Barrow-Green: Poincaré and the Three Body Problem. T. 11. Providence, Rhode Island: American Mathematical Society, 1996-10-29, seria: History of Mathematics. DOI: 10.1090/hmath/011. ISBN 978-0-8218-0367-7.

[28] V.V. Efimov V.V., Energy levels arising from resonant two-body forces in a three-body system (Poziomy energetyczne wynikające z rezonansowych sił dwuciałowych w układzie trzech ciał), „Physics Letters B”, 33 (8), 1970, s. 563–564, DOI: 10.1016/0370-2693(70)90349-7, Bibcode: 1970PhLB...33..563E (ang.).

[29] Shijun Liao, Xiaoming Li. O rozwiązaniach okresowych problemu trzech ciał. „National Science Review”. 6 (6), s. 1070–1071, 2019-11-01. DOI: 10.1093/nsr/nwz102. ISSN 2095-5138. PMID: 34691975. PMCID: PMC8291409.

[30] Philip G. Breen, Christopher N. Foley, Tjarda Boekholt, Simon Portegies Zwart. Newton versus the machine: Solving the chaotic three-body problem using deep neural networks (Newton kontra maszyna: Rozwiązywanie chaotycznego problemu trzech ciał za pomocą głębokich sieci neuronowych). „Monthly Notices of the Royal Astronomical Society”. 494 (2), s. 2465–2470, 2020. DOI: 10.1093/mnras/staa713. arXiv:1910.07291.

[SA-20230923-31] ClaireC. Watson ClaireC., We Just Got 12,000 New Solutions to The Infamous Three-Body Problem, [w:] ScienceAlert [online], 23 września 2023 [dostęp 2023-09-23] [zarchiwizowane z adresu 2023-09-24] .

[ARX-2023-32] Ivan Hristov, Radoslava Hristova, Veljko Dmitrašinović, Kiyotaka Tanikawa. Rewizja okresowych, bezkolizyjnych orbit swobodnego spadku dla trzech ciał o jednakowej masie. „Celestial Mechanics and Dynamical Astronomy”. 136 (1), 2024. DOI: 10.1007/s10569-023-10177-w. arXiv:2308.16159. Bibcode: 2024CeMDA.136....7H.

[33] Florin Diacu. "The Solution of the n-body Problem", The Mathematical Intelligencer, 1996.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]