Twierdzenie Pohlkego

Twierdzenie Pohlkego – podstawowe twierdzenie z aksonometrii^[1], które sformułował Karl Wilhelm Pohlke w 1853 r., a udowodnił Hermann Schwarz^[2][3] .

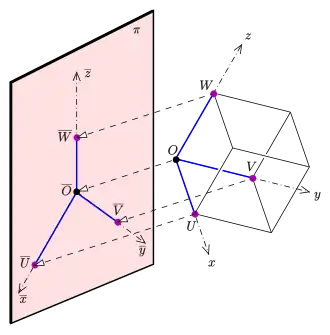
Trzy dowolne odcinki na płaszczyźnie ${\displaystyle {\overline {O}}{\overline {U}},}$ ${\displaystyle {\overline {O}}{\overline {V}}}$ i ${\displaystyle {\overline {O}}{\overline {W}}}$ wychodzące z jednego punktu ${\displaystyle {\overline {O}},}$ które nie leżą na jednej prostej, można rozważać jako rzut równoległy trzech krawędzi sześcianu ${\displaystyle OU,}$ ${\displaystyle OV}$ i ${\displaystyle OW}$^[4].

Zawartość twierdzenia Pohlkego stanowi podstawy teoretyczne metody aksonometrycznej^[1], czyli kreślenia figur geometrycznych w rzucie równoległym na płaszczyznę z użyciem układu wspólrzędnych^[5].

• dimetria prostokątna
• dimetria ukośna

• HermannH. Schwarz HermannH., Elementarer Beweis des Pohlkeschen Fundamentalsatzes der Axonometrie, „Journal für die reine und angewandte Mathematik”, 63, 1864, s. 309–314  (niem.).
• Matematyka, Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1990 (Encyklopedia szkolna), ISBN 83-02-02551-8 .

• EdwinE. Koźniewski EdwinE., Geometria odwzorowań inżynierskich. Wykład 01, „Scriptionis Geometrica”, I (1), 2014 [dostęp 2018-07-21] [zarchiwizowane z adresu 2018-07-22] . Brak numerów stron w czasopiśmie