Aksonometria
Aksonometria (gr. akson + metreo) – rodzaj rzutu równoległego, odwzorowanie przestrzeni na płaszczyznę z wykorzystaniem prostokątnego układu osi. Cechą odróżniającą aksonometrię od innych rodzajów rzutu równoległego jest dążenie do zachowania prawdziwych wymiarów rzutowanych obiektów przynajmniej w jednym, wybranym kierunku. Niektóre rodzaje aksonometrii pozwalają również zachować wielkości kątów, równoległych do obranej płaszczyzny[1].
Aksonometria jest szeroko stosowana w rysunku technicznym[2].
Podziały aksonometrii
Podział aksonometrii ze względu na kierunek rzutowanych osi układu prostokątnego:
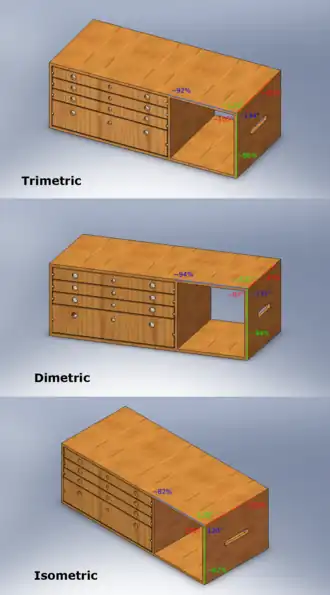
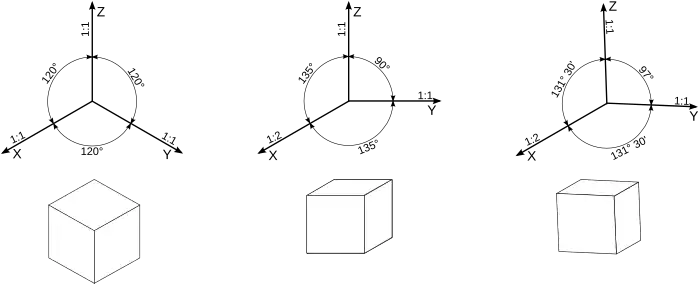
- izometria – wszystkie osie układu prostokątnego w przestrzeni tworzą jednakowy kąt z rzutnią i ich obrazy ulegają jednakowemu skrótowi – na rzutni powstaje obraz trzech osi tworzących pomiędzy sobą kąty po 120°, często na rysunkach izometrycznych pomija się wpływ skrótu;
- dimetria – dwie z osi układu prostokątnego tworzą z rzutnią jednakowe kąty (bywa, że są do niej równoległe), a zatem układ współrzędnych posiada jednakowe skróty na co najmniej dwóch osiach.
- trimetria (anizometria) – każda z osi układu prostokątnego tworzy z rzutnią inny kąt i podlega innemu skrótowi[1].
W aksonometrii obiekty trójwymiarowe odwzorowane są przez figury płaskie.
Zobacz też
Przypisy
- 1 2 3 4 Andrzej Bieliński: Geometria wykreślna. Politechnika Warszawska, 2005, s. 45-48, 57. ISBN 83-7207-564-6.
- ↑ aksonometria, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2024-10-24].
Linki zewnętrzne
 Axonometry (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2025-04-23].
Axonometry (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2025-04-23].