Twierdzenie o prostej prostopadłej do płaszczyzny
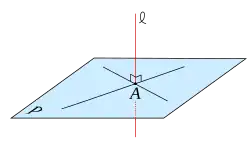
Twierdzenie o prostej prostopadłej do płaszczyzny – twierdzenie matematyczne w geometrii, konkretniej stereometrii. Mówi ono, że jeśli:
- dwie proste są współpłaszczyznowe i nierównoległe oraz
- inna prosta jest prostopadła do nich,
to ta trzecia prosta jest prostopadła do całej płaszczyzny, w której leżą dwie pierwsze[1][2]. Dowód tego faktu opiera się na własnościach trójkątów podobnych[1][3]. Fakt ten jest używany w dowodzie twierdzenia o trzech prostopadłych[4][5][6].
Twierdzenie to należy do podstawy programowej matematyki w polskich szkołach średnich w zakresie rozszerzonym[7].
Przypisy
- 1 2
Mariusz Plaszczyk, Twierdzenie o prostej prostopadłej do płaszczyzny, Zintegrowana Platforma Edukacyjna – Ministerstwo Edukacji Narodowej, zpe.gov.pl [dostęp 2024-10-24]. - ↑ Nowa Era 2022 ↓, s. 88.
- ↑ Nowa Era 2022 ↓, s. 90.
- ↑ Nowa Era 2022 ↓, s. 111.
- ↑ Adrian Karpowicz, Twierdzenie o 3 prostych prostopadłych, Zintegrowana Platforma Edukacyjna – Ministerstwo Edukacji Narodowej, zpe.gov.pl [dostęp 2024-10-28].
- ↑ Bartłomiej Bzdęga, Prostopadłość prostych w przestrzeni, „Delta”, listopad 2022, ISSN 0137-3005 [dostęp 2024-10-28].
- ↑ Podstawa programowa. Liceum ogólnokształcące i technikum. Matematyka, Zintegrowana Platforma Edukacyjna – Serwis Ministerstwa Edukacji Narodowej, zpe.gov.pl [dostęp 2024-10-24].
Bibliografia
- Wojciech Babiański, Lech Chańko, Joanna Czarnowska, Grzegorz Janocha, Jolanta Wesołowska: Matematyka 4. Podręcznik dla liceum ogólnokształcącego i technikum. Warszawa: Wydawnictwo Nowa Era, 2022. ISBN 978-83-267-4399-3.