Twierdzenie o trzech prostopadłych

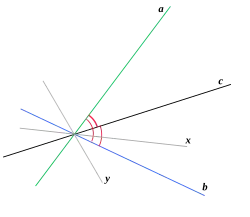
Twierdzenie o trzech prostopadłych – twierdzenie stereometrii: Jeżeli prosta b jest rzutem prostokątnym prostej a na daną płaszczyznę, to prosta c leżąca w tej płaszczyźnie jest prostopadła do prostej a wtedy i tylko wtedy, gdy jest prostopadła do b[1]:

Rysunek jest ilustracją twierdzenia:

  • proste x i y nie są prostopadłe do a, bo nie są prostopadłe do b, która jest rzutem a na płaszczyznę;
  • prosta c jest prostopadła do a, bo jest prostopadła do b.

Fakt ten można udowodnić, wykorzystując twierdzenie o prostej prostopadłej do płaszczyzny[2][3][4].

Przypisy

  1. ↑ publikacja w otwartym dostępie – możesz ją przeczytać Podstawa programowa. Liceum ogólnokształcące i technikum. Matematyka, Zintegrowana Platforma Edukacyjna – Serwis Ministerstwa Edukacji Narodowej, zpe.gov.pl [dostęp 2024-04-17].
  2. ↑ Nowa Era 2022 ↓, s. 111.
  3. ↑ publikacja w otwartym dostępie – możesz ją przeczytać Adrian Karpowicz, Twierdzenie o 3 prostych prostopadłych, Zintegrowana Platforma Edukacyjna – Ministerstwo Edukacji Narodowej, zpe.gov.pl [dostęp 2024-10-28].
  4. ↑ Bartłomiej Bzdęga, Prostopadłość prostych w przestrzeni, „Delta”, listopad 2022, ISSN 0137-3005 [dostęp 2024-10-28].

Bibliografia

  • Wojciech Babiański, Lech Chańko, Joanna Czarnowska, Grzegorz Janocha, Jolanta Wesołowska: Matematyka 4. Podręcznik dla liceum ogólnokształcącego i technikum. Warszawa: Wydawnictwo Nowa Era, 2022. ISBN 978-83-267-4399-3.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.