Dwudziesto-dwunastościan rombowy wielki
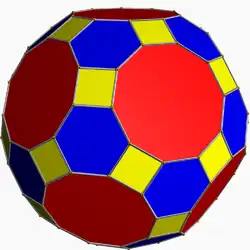
Dwudziesto-dwunastościan rombowy wielki – jeden z wielościanów archimedesowych, zbudowany z 62 ścian – 30 kwadratowych, 20 sześciokątnych i 12 dziesięciokątnych, ma 120 wierzchołków i 180 krawędzi.
Oznaczany jest symbolem Schläfliego i symbolem Wythoffa Wielościanem dualnym do tej bryły jest dwudziestościan szóstkowy[1][2][3][4][5][6][7].
Wśród wszystkich wielościanów archimedesowych o tej samej długości krawędzi, ta bryła ma największą objętość i pole powierzchni[1][2][3].
Wielościan jest zonościanem (ang. zonohedron)[1].
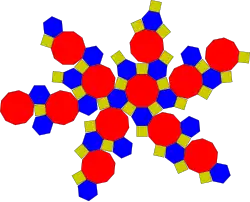
Bryłę tę skonstruował przy pomocy origami E. K. Herrstrom – konstrukcja wykorzystuje 900 jednostek sonobè[1].
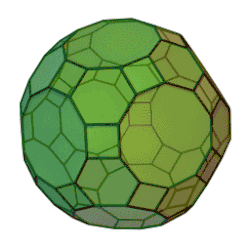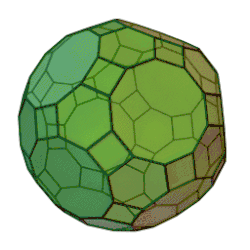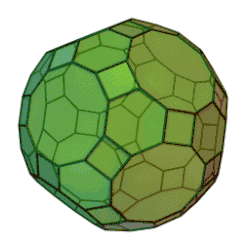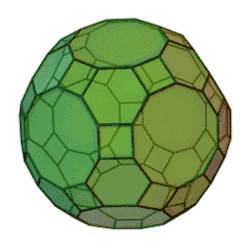
Wzory i właściwości
Niech będzie długością krawędzi bryły.
- Pole powierzchni całkowitej
[3], z czego wynika, że objętość kuli opisanej na bryle wynosi czyli około [3]
a więc objętość tej kuli można wyrazić wzorem i wynosi ona w przybliżeniu [3]
- Dystans normalny od środka bryły do jej ścian możemy wyrazić następującymi wzorami:
- dla ściany kwadratowej [3]
- dla ściany sześciokątnej [3]
- dla ściany dwunastokątnej [3]
- Niech oznacza odległość od krawędzi do środka bryły. Opiszmy na bryle dwunastościan, i oznaczmy jego krawędź jako dwudziestościan, którego krawędź oznaczymy jako oraz trzydziestościan rombowy, którego przekątna dłuższej ściany będzie posiadała oznaczenie Zachodzą wtedy następujące równości:
Powiązane obiekty
Z bryłą powiązanych jest wiele innych obiektów geometrycznych: wielościany z [5, 3] grupy Coxetera, parkietaże: euklidesowy, hiperboliczny, sferyczny. Istnieją też różne rzuty bryły i owych parkietaży[1][2][3]. Z bryła powiązany jest graf.
Graf
Ilustracja przedstawia graf zero-symetryczny utworzony z bryły[8].
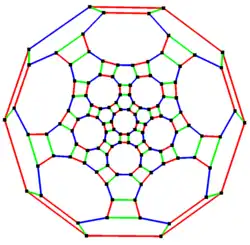
Powiązane wielościany i parkietaże
Dwudziesto-dwunastościan rombowy wielki jest elementem ciągu wielościanów rombowych i parkietaży, których grupa symetrii jest [5, 3] grupą Coxetera[1][2][3].
| Wielościan | Parkietaż euklidesowy | Parkietaż hiperboliczny | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Diagram Coextera | [5, 3] | t[5, 3] | r[5, 3] | t[3, 5] | [3, 5] | rr[5, 3] | tr[5, 3] | [6, 3] | [7, 3] | [8, 3] |
| Odpowiadający obiekt |  Dwunastościan Dwunastościan |
 Dwunastościan ścięty Dwunastościan ścięty |
 Dwudziesto-dwunastościan Dwudziesto-dwunastościan |
 Dwudziestościan ścięty Dwudziestościan ścięty |
 Dwudziestościan Dwudziestościan |
 Dwudziesto-dwunastościan rombowy mały Dwudziesto-dwunastościan rombowy mały |
Dwudziesto-dwunastościan rombowy wielki |  |
 |
 |
Rzuty ortogonalne
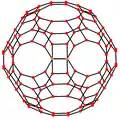
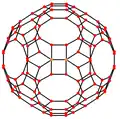
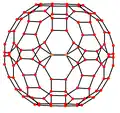
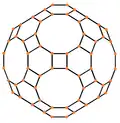
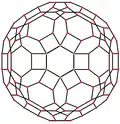
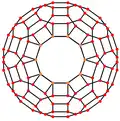
Przykłady kilku rzutów ortogonalnych dwudziesto-dwunastościanu rombowego wielkiego.Wycentrowane na wierzchołek, trzy typy krawędzi oraz trzy rodzaje ścian bryły[3].
| Rzuty ortogonalne bryły | |||||||
|---|---|---|---|---|---|---|---|
| Rzut wycentrowany na | Wierzchołek | Krawędzie 4-6 |
Krawędzie 4-10 |
Krawędzie 6-10 |
Ściana kwadratowa | Ściana sześciokątna | Ściana dziesięciokątna |
| Obraz | 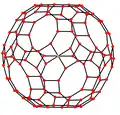 |
 |
 |
 |
 |
 |
 |
Parkietaże sferyczne i diagramy Schlegela
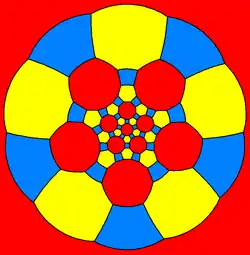
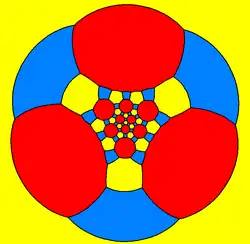
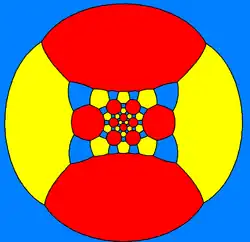
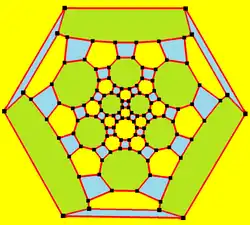
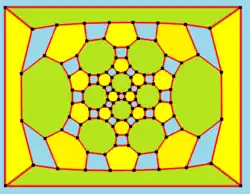
Dwudziesto-dwunastościan rombowy wielki może być też ukazany jako element parkietażu sferycznego oraz podobnego diagramu Schlegela.
| Bryła jako parkietaż sferyczny i diagram Schlegela, oraz rzuty tych obiektów | ||||
|---|---|---|---|---|
| Rzut ortograficzny | R. stereograficzny wycentrowany na: | |||
| dziesięciokąt | sześciokąt | kwadrat | ||
| Jako parkietaż sferyczny |
 |
 |
 |
 |
| Jako diagram Schlegela |
 |
 |
 |
 |
Przypisy
- 1 2 3 4 5 6 7 8 Eric W. Weisstein, Great Rhombicosidodecahedron, [w:] MathWorld, Wolfram Research (ang.).
- 1 2 3 4 The Great Rhombicosidodecahedron [online], eusebeia.dyndns.org [dostęp 2017-07-03] (ang.).
- 1 2 3 4 5 6 7 8 9 10 11 12 13 Harish Chandra Rajpoot, Mathematical analysis of great rhombicosidodecahedron (the largest Ar...) [online], 19 marca 2015 [dostęp 2017-07-03].
- ↑ graniastosłupy [online], www.zobaczycmatematyke.krk.pl [dostęp 2017-07-03].
- ↑ Dwudziesto-dwunastościan rombowy wielki – bryłyplatońskie [online], sites.google.com [dostęp 2017-07-03].
- 1 2 3 4 5 6 Robert Whittaker, The Great Rhombicosidodecahedron | polyhedra.mathmos.net [online], polyhedra.mathmos.net [dostęp 2017-07-11] (ang.).
- ↑ great rhombicosidodecahedron [online], bulatov.org [dostęp 2017-07-11].
- ↑ R.C Read, R.J. Wilson: An Atlas of Graphs. Oxford University Press, 1998, s. 269.
Linki zewnętrzne
Informacje o bryle
- Dogłębna analiza autorstwa H.Ch. Rajpoota
- http://polyhedra.mathmos.net/entry/greatrhombicosidodecahedron.html – Informacje przeglądowe, stosunki krawędzi do opisanych brył
- http://bulatov.org/polyhedra/uniform/u72.html – Podstawowe informacje i ilustracja
Strony z siatką bryły do wydruku
- http://www.korthalsaltes.com/model.php?name_en=rhombicosidodecahedron
- http://www.maths-pro.com/New%20Polyhedra%20books/Polyhedra%20book%202012%20GPP%20-%20V6.pdf Plik w formacie PDF, siatki i porady umieszczone są na stronach 31, 33, 85