MSK (modulacja)

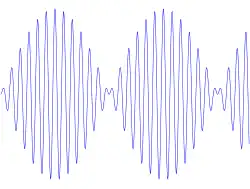
MSK (ang. Minimum Shift Keying) – odmiana modulacji FSK fal elektromagnetycznych stosowana do przesyłu informacji w telekomunikacji. Jest to w praktyce modulacja CPFSK (ang. Continuous Phase FSK), czyli kluczowanie częstotliwości z ciągłą fazą. Charakteryzuje się dobrymi właściwościami energetycznymi.

W cyfrowej modulacji częstotliwościowej, wartościom „0” i „1” odpowiadają dwa sygnały o różnych częstotliwościach:

${\displaystyle S_{1}(t)=A\cos[\omega _{1}t+\phi (0)]\quad {}}$ (1a)

${\displaystyle S_{0}(t)=A\cos[\omega _{2}t+\phi (0)]\quad {}}$ (1b)

gdzie:

${\displaystyle \phi (0)}$ jest fazą początkową sygnału (dla ${\displaystyle t=0}$).

Dla modulacji MSK, można wyrazić wzór ogólny sygnału zmodulowanego:

${\displaystyle S(t)=A\cos[\omega _{0}t+\phi (t)]\quad {}}$ (2)

gdzie:

${\displaystyle \phi (t)=\phi (0)+at}$ dla sygnału „1” oraz ${\displaystyle \phi (t)=\phi (0)-at}$ dla sygnału „0”.

We wzorze tym, zmienną ${\displaystyle a,}$ zwaną indeksem modulacji, definiuje się następująco:

${\displaystyle a={\frac {\pi }{T_{b}}}h,}$ co przy założeniu ${\displaystyle h=T_{b}(f_{1}-f_{2})}$ sprowadza się do postaci:

${\displaystyle a={\frac {\pi }{T_{b}}}T_{b}(f_{1}-f_{2})={\frac {1}{2}}(\omega _{1}-\omega _{2})}$

wtedy:

${\displaystyle \phi (t)=\phi (0)\pm {\frac {1}{2}}(\omega _{1}-\omega _{2})t.\quad {}}$ (3)

Jeśli założy się ${\displaystyle \omega _{0}={\frac {1}{2}}(\omega _{1}-\omega _{2})}$ oraz, dla uproszczenia, przyjmie się fazę początkową równą 0, można sprowadzić zależność (2) do wzorów:

${\displaystyle S_{1}(t)=A\cos \left[{\frac {1}{2}}(\omega _{1}+\omega _{2})t+{\frac {1}{2}}(\omega _{1}-\omega _{2})t\right]=A\cos(\omega _{1}t),}$

${\displaystyle S_{0}(t)=A\cos \left[{\frac {1}{2}}(\omega _{1}+\omega _{2})t-{\frac {1}{2}}(\omega _{1}-\omega _{2})t\right]=A\cos(\omega _{2}t).}$

Aby zapewnić ortogonalność sygnałów reprezentujących „0” i „1”, należy tak dobrać częstotliwości ${\displaystyle f_{1}}$ i ${\displaystyle f_{2},}$ aby spełniały następujący warunek:

${\displaystyle \Delta fT_{b}=h={\frac {1}{2}}n,\quad n=1,2,3\dots }$

Jak widać ${\displaystyle n_{min}=1,}$ więc najmniejsza różnica częstotliwości, to różnica o pół cyklu w jednym okresie ${\displaystyle T_{b}.}$ Właśnie taki przypadek zachodzi w modulacji MSK.

Ostatecznie dla modulacji MSK można zapisać:

${\displaystyle \phi (t)=\phi (0)\pm {\frac {\pi }{2T_{b}}}t,}$

${\displaystyle S(t)=A\cos \phi (t)\cos(\omega _{0}t)-A\sin \phi (t)\sin(\omega _{0}t),}$

człon ${\displaystyle \cos \phi (t)}$ nazywa się składową synfazową i oznaczany jest poprzez I(t), a człon ${\displaystyle \sin \phi (t)}$ – składową kwadraturową Q(t).

Fazę sygnału zmodulowanego można odczytać z tzw. wykresu kratowego fazy:

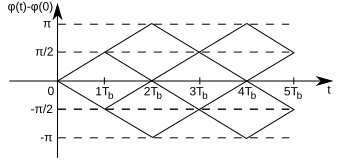
Przykład wykorzystania wykresu kratowego:

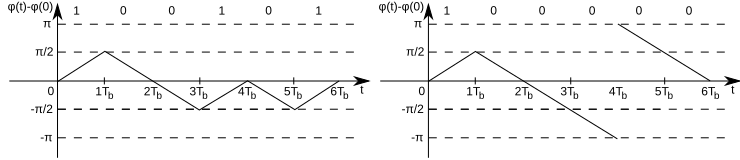
Jak widać z wykresu kratowego, dla parzystych bitów faza początkowa wynosić może 0, ${\displaystyle \pi }$ lub ${\displaystyle -\pi ,}$ wtedy:

${\displaystyle \phi (0)=0\Rightarrow I(t)=\cos \left({\frac {\pi }{2T_{b}}}t\right),}$

${\displaystyle \phi (0)=\pi \vee \phi (0)=-\pi \Rightarrow I(t)=-\cos \left({\frac {\pi }{2T_{b}}}t\right).}$

Dla nieparzystych bitów, faza początkowa może wynosić ${\displaystyle +\pi /2}$ lub ${\displaystyle -\pi /2{:}}$

${\displaystyle \phi (T_{b})=+{\frac {\pi }{2}}\Rightarrow Q(t)=\sin \left({\frac {\pi }{2T_{b}}}t\right),}$

${\displaystyle \phi (T_{b})=-{\frac {\pi }{2}}\Rightarrow Q(t)=-\sin \left({\frac {\pi }{2T_{b}}}t\right).}$

Aby określić diagram konstalacji modulacji MSK, zapisać można sygnał zmodulowany w postaci:

${\displaystyle S(t)={\sqrt {E_{b}}}\Phi _{1}(t)-{\sqrt {E_{b}}}\Phi _{2}(t),}$

we wzorze tym:

${\displaystyle \Phi _{1}(t)={\sqrt {\frac {2}{Tb}}}\cos \phi (t)\cos(\omega _{0}t),}$

${\displaystyle \Phi _{2}(t)={\sqrt {\frac {2}{Tb}}}\sin \phi (t)\sin(\omega _{0}t).}$

	${\displaystyle \phi (0)}$	znak ${\displaystyle \Phi _{1}}$	${\displaystyle \phi (T_{b})}$	znak ${\displaystyle \Phi _{2}}$	znak ${\displaystyle -\Phi _{2}}$	Przesyłane bity
1	0	+	${\displaystyle \pi /2}$	+	–	1
2	${\displaystyle \pi }$	–	${\displaystyle \pi /2}$	+	–	0
3	${\displaystyle \pi }$	–	${\displaystyle -\pi /2}$	–	+	1
4	0	+	${\displaystyle -\pi /2}$	–	+	0

Na podstawie powyższej tabeli, utworzyć można diagram konstelacji dla modulacji MSK:

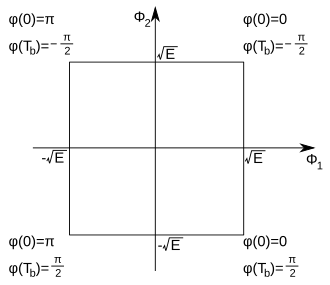
Modulację MSK cechuje dużo węższe widmo częstotliwościowe niż QPSK/BPSK. MSK jest więc znacznie oszczędniejsza energetycznie. Dzięki temu jest powszechnie stosowana w telekomunikacji (zwłaszcza GMSK). Schemat modulatora MSK:

Sygnał na wejściu filtrów pasmowych:

${\displaystyle y(t)=\cos \omega _{0}t\cos \left({\frac {\pi }{2T_{b}}}t\right)={\frac {1}{2}}\cos \left[\left(\omega _{0}-{\frac {\pi }{2T_{b}}}\right)t\right]+{\frac {1}{2}}\cos \left[\left(\omega _{0}+{\frac {\pi }{2T_{b}}}\right)t\right]}$

${\displaystyle \Phi _{1}(t)={\frac {1}{2}}\cos \left[\left(\omega _{0}+{\frac {\pi }{2T_{b}}}\right)t\right]+{\frac {1}{2}}\cos \left[\left(\omega _{0}+{\frac {\pi }{2T_{b}}}\right)t\right]=\cos \left({\frac {\pi }{2T_{b}}}t\right)\cos(\omega _{0}t)}$

${\displaystyle \Phi _{1}(t)={\frac {1}{2}}\cos \left[\left(\omega _{0}-{\frac {\pi }{2T_{b}}}\right)t\right]+{\frac {1}{2}}\cos \left[\left(\omega _{0}+{\frac {\pi }{2T_{b}}}\right)t\right]=\sin \left({\frac {\pi }{2T_{b}}}t\right)\sin(\omega _{0}t)}$

${\displaystyle S(t)=m_{I}(t)\cos \left({\frac {\pi }{2T_{b}}}t\right)\cos(\omega _{0}t)-m_{Q}(t)\sin \left({\frac {\pi }{2T_{b}}}t\right)\sin(\omega _{0}t).}$

• GMSK