Twierdzenie Cauchy’ego (rachunek różniczkowy)

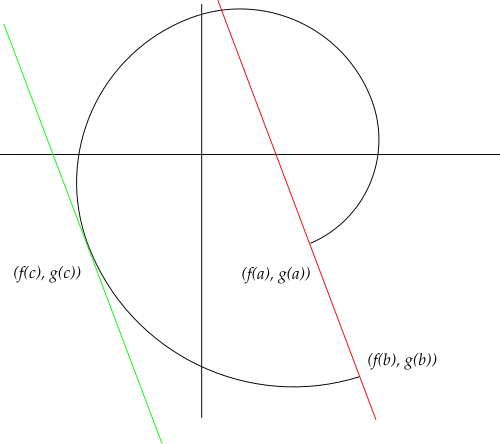
Twierdzenie Cauchy’ego, uogólnione twierdzenie o wartości średniej^[2] – twierdzenie w analizie matematycznej, konkretniej w analizie rzeczywistej i rachunku różniczkowym, zaliczane do twierdzeń o wartości średniej. Mówi, że jeśli dwie funkcje rzeczywiste na przedziale są różniczkowalne, to istnieje w tym przedziale punkt, dla którego pewne wyrażenia są równe.

Jest to uogólnienie twierdzenia Lagrange’a o wartości średniej^[3][4][1], a przez to – twierdzenia Rolle’a. Zastosowania twierdzenia Cauchy’ego to między innymi:

• oszacowanie błędu (reszty) we wzorze Taylora^[5][6];
• dowód reguły de l’Hospitala^[7][8].

Jeżeli dane funkcje ${\displaystyle f}$ i ${\displaystyle g}$ są:

• ciągłe w przedziale domkniętym ${\displaystyle [a,b],}$
• różniczkowalne w przedziale ${\displaystyle (a,b),}$

to istnieje punkt ${\displaystyle c}$ należący do przedziału ${\displaystyle (a,b)}$ taki, że^[4]:

${\displaystyle g'(c)\cdot \left[f(b)-f(a)\right]=f'(c)\cdot \left[g(b)-g(a)\right].}$

Zdefiniujmy ${\displaystyle h:[a,b]\to \mathbb {R} }$

${\displaystyle h(x)=(f(b)-f(a))g(x)-(g(b)-g(a))f(x).}$

Zauważmy, że ${\displaystyle h}$ jest różniczkowalna na ${\displaystyle (a,b)}$ oraz ${\displaystyle h(a)=h(b),}$ więc na mocy twierdzenia Rolle’a istnieje ${\displaystyle c\in (a,b)}$ takie, że ${\displaystyle h'(c)=0.}$ Ponadto

${\displaystyle 0=h'(c)=(f(b)-f(a))g'(c)-(g(b)-g(a))f'(c),}$

co kończy dowód.

Jeżeli funkcje ${\displaystyle f}$ i ${\displaystyle g}$ są:

• ciągłe w przedziale domkniętym ${\displaystyle [a,b],}$ różniczkowalne w przedziale ${\displaystyle (a,b)}$ oraz dodatkowo ${\displaystyle g'(x)\not =0}$ dla ${\displaystyle x\in (a,b),}$

to istnieje taki punkt ${\displaystyle c\in (a,b),}$ że^[9][1]:

${\displaystyle {\frac {f(b)-f(a)}{g(b)-g(a)}}={\frac {f'(c)}{g'(c)}}.}$

• Grigorij Michajłowicz Fichtenholz: Rachunek różniczkowy i całkowy. Tom 1. Warszawa: Wydawnictwo Naukowe PWN, 1994. ISBN 83-01-02175-6.
• Franciszek Leja: Rachunek różniczkowy i całkowy ze wstępem do równań różniczkowych. Wyd. VI. Warszawa: Państwowe Wydawnictwo Naukowe, 1963, seria: Biblioteka Matematyczna, tom 2.
• Ryszard Rudnicki: Wykłady z analizy matematycznej. Warszawa: Wydawnictwo Naukowe PWN, 2006. ISBN 978-83-01-14946-8.
• PawełP. Strzelecki PawełP., Analiza matematyczna I (skrypt wykładu) [online], mimuw.edu.pl, 14 grudnia 2018 [dostęp 2024-07-08] .

• Walter Rudin: Principles of Mathematical Analysis. McGraw-Hill, 1976, s. 107–108. ISBN 0-07-054235-X.

• Eric W.E.W. Weisstein Eric W.E.W., Extended Mean-Value Theorem, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2022-06-20].
• Cauchy theorem (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2022-08-06].