Wielomiany Legendre’a

Wielomiany Legendre’a (nieunormowane) – wielomiany określone wzorem (Rodriguesa)

${\displaystyle P_{n}={\frac {1}{2^{n}n!}}{\frac {d^{n}}{dx^{n}}}(x^{2}-1)^{n}\quad (n=0,1,\dots ).}$

Można je również zapisać w jawnej postaci

${\displaystyle P_{n}(x)={\frac {1}{2^{n}}}\sum _{i=0}^{[{\frac {n}{2}}]}(-1)^{i}{n \choose i}{2n-2i \choose n}x^{n-2i}.}$

Ich nazwa pochodzi od nazwiska Adriena-Marie Legendre’a.

Wielomiany Legendre’a są współczynnikami w rozwinięciu w szereg Maclaurina funkcji G(x,t) postaci:

${\displaystyle G(x,t)=(1-2xt+t^{2})^{-1/2}.}$

Zachodzi wzór:

${\displaystyle G(x,t)=(1-2xt+t^{2})^{-1/2}=\sum _{l=0}^{\infty }P_{l}(x)t^{l}.}$

• zależność rekurencyjna

${\displaystyle P_{n+1}(x)={\frac {2n+1}{n+1}}xP_{n}(x)-{\frac {n}{n+1}}P_{n-1}(x)\quad (n=1,2,\dots ).}$

• ortogonalność z wagą ${\displaystyle p(x)=1}$ na odcinku ${\displaystyle [-1,1]}$
• ${\displaystyle \int _{-1}^{1}P_{m}(x)P_{n}(x)dx={\frac {2}{2n+1}}\delta _{mn},}$ a zatem układ ${\displaystyle \{{\sqrt {n+{\tfrac {1}{2}}}}P_{n}\colon \,n\in \mathbb {N} \}}$ jest układem ortonormalnym w przedziale [-1,1].

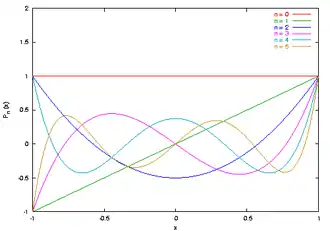Poniżej wymieniono kilka początkowych wielomianów Legendre’a:

${\displaystyle P_{0}(x)=1}$

${\displaystyle P_{1}(x)=x}$

${\displaystyle P_{2}(x)={\tfrac {1}{2}}(3x^{2}-1)}$

${\displaystyle P_{3}(x)={\tfrac {1}{2}}(5x^{3}-3x)}$

${\displaystyle P_{4}(x)={\tfrac {1}{8}}(35x^{4}-30x^{2}+3)}$

${\displaystyle P_{5}(x)={\tfrac {1}{8}}(63x^{5}-70x^{3}+15x)}$

${\displaystyle P_{6}(x)={\tfrac {1}{16}}(231x^{6}-315x^{4}+105x^{2}-5)}$

${\displaystyle P_{7}(x)={\tfrac {1}{16}}(429x^{7}-693x^{5}+315x^{3}-35x)}$

${\displaystyle P_{8}(x)={\tfrac {1}{128}}(6435x^{8}-12012x^{6}+6930x^{4}-1260x^{2}+35)}$

${\displaystyle P_{9}(x)={\tfrac {1}{128}}(12155x^{9}-25740x^{7}+18018x^{5}-4620x^{3}+315x)}$

${\displaystyle P_{10}(x)={\tfrac {1}{256}}(46189x^{10}-109395x^{8}+90090x^{6}-30030x^{4}+3465x^{2}-63)}$

${\displaystyle P_{11}(x)={\tfrac {1}{256}}(88179x^{11}-230945x^{9}+218790x^{7}-90090x^{5}+15015x^{3}-693x)}$

Z wielomianami Legendre’a związane są stowarzyszone funkcje Legendre’a

• formuła trójczłonowa
• wielomiany Czebyszewa
• wielomiany Hermite’a
• wielomiany Laguerre’a

• Grigorij Michajłowicz Fichtenholz: Rachunek różniczkowy i całkowy, t. 3. Warszawa: Państwowe Wydawnictwo Naukowe, 1966, s. 354.