Hipoteza Riemanna

Hipoteza Riemanna – sformułowana w 1859 roku hipoteza^[1], dotycząca badanej przez niemieckiego matematyka Bernharda Riemanna funkcji dzeta. Mówi ona, że wszystkie nietrywialne (tj. nierzeczywiste) miejsca zerowe tej funkcji mają część rzeczywistą równą ${\displaystyle {\frac {1}{2}}}$^[2].
Hipoteza Riemanna pozostaje – obok hipotezy Goldbacha – jednym z największych nierozwiązanych problemów w matematyce. Ma ona duże znaczenie dla całej matematyki – w szczególności dla teorii liczb, ale również dla statystyki oraz fizyki.
Hipoteza Riemanna jest ósmym problemem na liście problemów Hilberta. Jest również jednym z problemów milenijnych, ogłoszonych w 2000 roku przez Instytut Matematyczny Claya^[3], który ufundował nagrodę w wysokości miliona dolarów za podanie dowodu lub obalenie tej hipotezy.

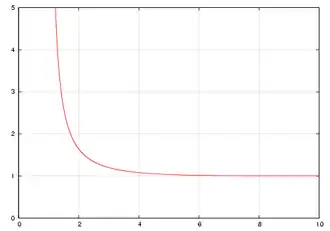
Dla liczb zespolonych ${\displaystyle s}$ spełniających warunek ${\displaystyle \operatorname {Re} s>1}$ funkcja dzeta określona jest wzorem:

${\displaystyle \zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}.}$

Funkcja ta daje się jednoznacznie przedłużyć analitycznie na całą płaszczyznę zespoloną, nie licząc punktu ${\displaystyle s=1}$, gdzie funkcja przechodzi w rozbieżny szereg harmoniczny. Wtedy funkcja dzeta spełnia równanie funkcyjne:

${\displaystyle \zeta (s)=2^{s}\pi ^{s-1}\ \sin \left({\frac {\pi s}{2}}\right)\ \Gamma (1-s)\ \zeta (1-s),}$

gdzie ${\displaystyle \mathrm {\Gamma } (s)}$ reprezentuje funkcję gamma. Dzięki temu rozszerzeniu funkcja dzeta ma trywialne miejsca zerowe dla ${\displaystyle s=-2,-4,-6,...}$, wynikające z zerowania się funkcji sinus.
(Uwaga: dla ${\displaystyle s=2,4,6,...}$ stosuje się pierwotną postać szeregu zbieżnego w tym przypadku do od lat znanych wartości (różnych od zera) pokazanych choćby przez Eulera).
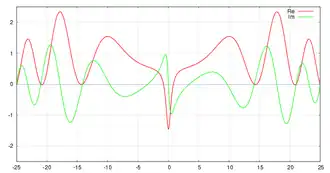
Hipoteza Riemanna mówi, że wszystkie pozostałe miejsca zerowe znajdują się na prostej ${\displaystyle \operatorname {Re} s={\frac {1}{2}}}$, zwanej prostą krytyczną. G.H. Hardy oraz J.E. Littlewood udowodnili, że istnieje nieskończenie wiele miejsc zerowych funkcji dzeta na prostej krytycznej. Zostało również udowodnione, że przynajmniej 40% miejsc zerowych leży na prostej krytycznej (Conrey, 1989).

Prawdziwość hipotezy Riemanna pozwalałaby na wzmocnienie pewnych nierówności dotyczących liczb pierwszych oraz równości asymptotycznych. Okazuje się na przykład, że hipoteza Riemanna jest równoważna poniższej równości (π(n) to liczba liczb pierwszych w przedziale od 1 do n), będącej wzmocnieniem twierdzenia o liczbach pierwszych:

${\displaystyle \pi (n)=\mathrm {Li} (n)+O\left({\sqrt {n}}\ln n\right)}$

gdzie ${\displaystyle \mathrm {Li} (n)}$ oznacza resztę z logarytmu całkowego, a do zapisu użyto tzw. dużego O.

Polskojęzyczne

Nagrania na YouTube [dostęp 2025-05-12]:

• Tomasz Miller, Czego uczy nas hipoteza Riemanna?, Centrum Kopernika Badań Interdyscyplinarnych – Uniwersytet Jagielloński (CKBI UJ), kanał „Copernicus” , 15 listopada 2018.
• Paweł Strzelecki, Hipoteza Riemanna, seria: Maraton wykładowy z „Deltą”, kanał „Wszechnica FWW”, 9 marca 2021.
• Tomasz Rożek, Ten matematyczny problem przyprawia o szaleństwo – hipoteza Riemanna, kanał „Nauka. To Lubię”, 8 maja 2025.

Anglojęzyczne

• Eric W.E.W. Weisstein Eric W.E.W., Riemann Zeta Function, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12]  (ang.).
• Riemann hypotheses (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2023-06-18].
• Alex Kontorovich, The Riemann Hypothesis, Explained, kanał Quanta Magazine na YouTube, 4 stycznia 2021 [dostęp 2023-06-08].