Definicje
Funkcje sinus i kosinus można definiować sobą nawzajem, przez wzór[1]:

Jest on znany jako jedynka trygonometryczna, a artykuł o niej podaje też dwie odmiany tej tożsamości. Oprócz tego za pomocą funkcji sinus i kosinus definiuje się tangens i kotangens[1]:



Okresowość funkcji
Funkcje trygonometryczne są okresowe[1] – dla dowolnej liczby całkowitej 


Parzystość i nieparzystość funkcji trygonometrycznych

Zależności pomiędzy funkcjami a kofunkcjami
Równości
![{\displaystyle {\begin{aligned}&\sin x=\cos \left({\frac {\pi }{2}}-x\right)&&\cos x=\sin \left({\frac {\pi }{2}}-x\right)\\[.2em]&\operatorname {tg} x=\operatorname {ctg} \left({\frac {\pi }{2}}-x\right)&&\operatorname {ctg} x=\operatorname {tg} \left({\frac {\pi }{2}}-x\right)\\[.2em]&\sec x=\operatorname {cosec} \left({\frac {\pi }{2}}-x\right)&&\operatorname {cosec} x=\sec \left({\frac {\pi }{2}}-x\right)\end{aligned}}}](./bfd95bdb88e651940e908933f83dcad199334479.svg)
nazywa się związkami pomiędzy funkcjami a ich kofunkcjami. Kofunkcją sinusa jest cosinus, cosinusa sinus, tangensa cotangens itd.
Odwrotności
Funkcje trygonometryczne można układać w pary według kofunkcji lub według odwrotności. Odwrotnością sinusa jest cosecans, cosinusa secans, tangensa cotangens (i oczywiście na odwrót):
![{\displaystyle {\begin{aligned}&\sin x={\frac {1}{\operatorname {cosec} x}}&&\operatorname {cosec} x={\frac {1}{\sin x}}\\[.5em]&\cos x={\frac {1}{\sec x}}&&\sec x={\frac {1}{\cos x}}\\[.5em]&\operatorname {tg} x={\frac {1}{\operatorname {ctg} x}}&&\operatorname {ctg} x={\frac {1}{\operatorname {tg} x}}\end{aligned}}}](./c997a622134bd906219470948bb3121aa2633ce5.svg)
Funkcje wielokrotności kątów
Wzory ogólne
Można je znaleźć przez rekurencyjne stosowanie wzorów na funkcje sumy kątów[5].
![{\displaystyle {\begin{aligned}\sin nx&=\sum _{i=0}^{\infty }(-1)^{i}\cdot {n \choose 2i+1}\cos ^{n-2i-1}x\sin ^{2i+1}x\\[2pt]&=\sum _{i=0}^{\lfloor {\frac {n}{2}}\rfloor }(-1)^{i}\cdot {n \choose 2i+1}\cos ^{n-2i-1}x\sin ^{2i+1}x\\&=n\cos ^{n-1}x\sin x-{n \choose 3}\cos ^{n-3}x\sin ^{3}x+{n \choose 5}\cos ^{n-5}x\sin ^{5}x-{n \choose 7}\cos ^{n-7}x\sin ^{7}x+\dots \end{aligned}}}](./714e1218d101c47c2664961856dd7d3326ba7738.svg)
![{\displaystyle {\begin{aligned}\cos nx&=\sum _{i=0}^{\infty }(-1)^{i}\cdot {n \choose 2i}\cos ^{n-2i}x\sin ^{2i}x\\[2pt]&=\sum _{i=0}^{\lfloor {\frac {n}{2}}\rfloor }(-1)^{i}\cdot {n \choose 2i}\cos ^{n-2i}x\sin ^{2i}x\\&=\cos ^{n}x-{n \choose 2}\cos ^{n-2}x\sin ^{2}x+{n \choose 4}\cos ^{n-4}x\sin ^{4}x-{n \choose 6}\cos ^{n-6}x\sin ^{6}x+\dots \end{aligned}}}](./3eb40d217ed38a880497203d0468cb9a544202f5.svg)

Iloczyn w postaci sumy
Iloczyny dwóch funkcji
Źródła[1][9]:



Potęgi w postaci sumy
Źródło większości wzorów[10]:
Sześciany


Czwarte potęgi


Funkcje trygonometryczne wyrażone przy pomocy tangensa połowy kąta



Powyższe tożsamości znalazły zastosowanie w tzw. podstawieniu uniwersalnym, stosowanym przy obliczaniu całek typu  gdzie
gdzie  jest funkcją wymierną zmiennych
jest funkcją wymierną zmiennych  Stosuje się podstawienie:
Stosuje się podstawienie:



Inne zależności między funkcjami trygonometrycznymi

Wzór de Moivre’a

lub ogólniej:
![{\displaystyle [r(\cos x+i\sin x)]^{n}=r^{n}(\cos nx+i\sin nx)\qquad n\in \mathbb {N} }](./76357c43423817aec6638c42c3dfecbcfbbcfde5.svg)
Przypisy
- 1 2 3 4 5 6 funkcje trygonometryczne, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2025-05-02] .
- ↑ JoannaJ. Jaszuńska JoannaJ., Trygonometria obrazkowa, „Delta”, kwiecień 2014, ISSN 0137-3005 [dostęp 2024-10-30] .
- ↑ Eric W.E.W. Weisstein Eric W.E.W., Trigonometric Addition Formulas, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2025-04-29].
- ↑ Eric W.E.W. Weisstein Eric W.E.W., Double-Angle Formulas, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2025-04-29].
- 1 2 3 Eric W.E.W. Weisstein Eric W.E.W., Multiple-Angle Formulas, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2025-04-29].
- ↑ Eric W.E.W. Weisstein Eric W.E.W., Half-Angle Formulas, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2025-04-29].
- ↑
 Zastosowanie wzorów na sumę i różnicę funkcji trygonometrycznych do dowodzenia tożsamości trygonometrycznych, Zintegrowana Platforma Edukacyjna – Ministerstwo Edukacji Narodowej (ZPE MEN), zpe.gov.pl [dostęp 2025-05-02].
Zastosowanie wzorów na sumę i różnicę funkcji trygonometrycznych do dowodzenia tożsamości trygonometrycznych, Zintegrowana Platforma Edukacyjna – Ministerstwo Edukacji Narodowej (ZPE MEN), zpe.gov.pl [dostęp 2025-05-02].
- ↑ Eric W.E.W. Weisstein Eric W.E.W., Prosthaphaeresis Formulas, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2025-04-29].
- ↑ Eric W.E.W. Weisstein Eric W.E.W., Werner Formulas, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2025-04-29].
- ↑ Eric W.E.W. Weisstein Eric W.E.W., Trigonometric Power Formulas, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2025-04-29].
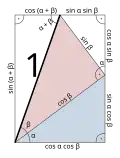 Sinus i cosinus sumy kątów
Sinus i cosinus sumy kątów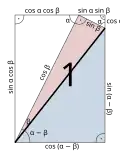 Sinus i cosinus różnicy kątów
Sinus i cosinus różnicy kątów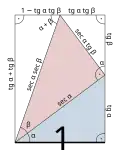 Tangens sumy kątów
Tangens sumy kątów Tangens różnicy kątów
Tangens różnicy kątów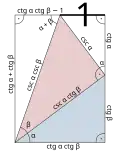 Cotangens sumy kątów
Cotangens sumy kątów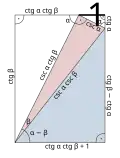 Cotangens różnicy kątów
Cotangens różnicy kątów Zastosowanie wzorów na sumę i różnicę funkcji trygonometrycznych do dowodzenia tożsamości trygonometrycznych, Zintegrowana Platforma Edukacyjna – Ministerstwo Edukacji Narodowej (ZPE MEN), zpe.gov.pl [dostęp 2025-05-02].
Zastosowanie wzorów na sumę i różnicę funkcji trygonometrycznych do dowodzenia tożsamości trygonometrycznych, Zintegrowana Platforma Edukacyjna – Ministerstwo Edukacji Narodowej (ZPE MEN), zpe.gov.pl [dostęp 2025-05-02]. Paweł Lubowiecki, Funkcje trygonometryczne cz. IV Tożsamości trygonometryczne, Wojskowa Akademia Techniczna im. Jarosława Dąbrowskiego, kanał „Uczelnia WAT” na YouTube, 30 stycznia 2024 [dostęp 2024-09-07].
Paweł Lubowiecki, Funkcje trygonometryczne cz. IV Tożsamości trygonometryczne, Wojskowa Akademia Techniczna im. Jarosława Dąbrowskiego, kanał „Uczelnia WAT” na YouTube, 30 stycznia 2024 [dostęp 2024-09-07].