Funkcja potęgowa

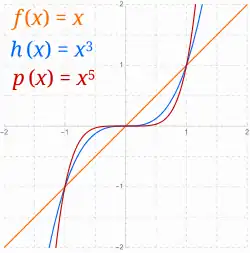
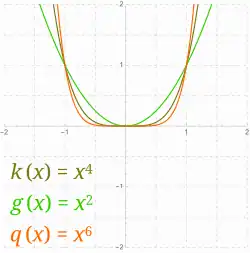
Funkcja potęgowa – typ funkcji matematycznej, definiowany różnie, zwykle jako rodzaj funkcji rzeczywistej zmiennej rzeczywistej:

• w sensie ścisłym, łac. sensu stricto, jest to dowolna funkcja potęgująca swoje argumenty; innymi słowy to potęga, gdzie argument funkcji jest podstawą – tak rozumiana funkcja potęgowa jest postaci ${\displaystyle x\mapsto x^{k},\ k\in \mathbb {R} }$^[1];
• w sensie szerokim, łac. sensu largo, jest to uogólnienie powyższego pojęcia i wzoru – dowolna funkcja postaci ${\displaystyle x\mapsto ax^{k},\ a,k\in \mathbb {R} }$^[2], czyli jednomian jednej zmiennej^[3].

Funkcje potęgowe mogą mieć różne dziedziny i zbiory wartości, co opisano niżej i przedstawiono na ilustracjach.

Do funkcji potęgowych należą między innymi^[4]:

• funkcja tożsamościowa ${\displaystyle (k=1);}$
• kwadrat liczby ${\displaystyle (k=2);}$
• sześcian liczby ${\displaystyle (k=3);}$
• liczba odwrotna ${\displaystyle (k=-1);}$
• pierwiastek kwadratowy ${\displaystyle (k=1/2);}$
• pierwiastek sześcienny ${\displaystyle (k=1/3);}$
• inne pierwiastkowanie.

Dla obu definicji dziedzina funkcji zależy od wykładnika, wyżej oznaczonego literą ${\displaystyle k\colon }$

• jeśli wykładnik jest naturalny i dodatni ${\displaystyle (k\in \mathbb {N} _{+}),}$ to dziedziną jest cały zbiór liczb rzeczywistych^[1]; takie funkcje potęgowe należą do funkcji wielomianowych;
• ${\displaystyle k=0}$ – dziedziną funkcji jest zbiór liczb rzeczywistych, funkcja przyjmuje postać funkcji stałej;
• jeśli wykładnik jest całkowity i ujemny ${\displaystyle (k\in \mathbb {Z} _{\leqslant -1}),}$ to dziedziną jest zbiór niezerowych liczb rzeczywistych^[1];
• ${\displaystyle k={\tfrac {n}{m}}>0,}$ dla całkowitych, względnie pierwszych liczb ${\displaystyle m,n}$ – dziedziną funkcji jest zbiór liczb rzeczywistych dla ${\displaystyle m}$ nieparzystych, dla ${\displaystyle m}$ parzystych dziedziną jest zbiór liczb rzeczywistych nieujemnych;
• ${\displaystyle k={\tfrac {n}{m}}<0,}$ dla całkowitych, względnie pierwszych liczb ${\displaystyle m,n}$ – dziedziną funkcji jest zbiór liczb rzeczywistych bez zera dla ${\displaystyle m}$ nieparzystych, dla ${\displaystyle m}$ parzystych dziedziną jest zbiór liczb rzeczywistych dodatnich;
• ${\displaystyle k\in \mathbb {R} \setminus \mathbb {Q} }$ – dla ${\displaystyle k}$ dodatnich dziedziną jest zbiór liczb rzeczywistych nieujemnych, dla ${\displaystyle k}$ ujemnych dziedziną jest zbiór liczb rzeczywistych dodatnich^[5].

Rozważa się też funkcje potęgowe o argumentach zespolonych^[6].

• Funkcja potęgowa, serwis „Matematyka z ZUT-em”, Zachodniopomorski Uniwersytet Technologiczny w Szczecinie, matematyka.zut.edu.pl [dostęp 2025-05-16].