Rozkład Cauchy’ego
Gęstość prawdopodobieństwa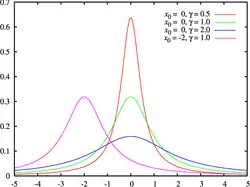 Zielona linia opisuje standardowy rozkład Cauchy’ego | |
Dystrybuanta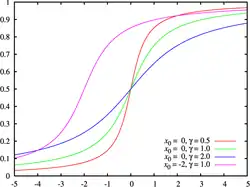 Kolory odpowiadają wykresowi powyżej | |
| Parametry |
– położenie (liczba rzeczywista) |
|---|---|
| Nośnik |
|
| Gęstość prawdopodobieństwa |
|
| Dystrybuanta |
|
| Wartość oczekiwana (średnia) |
nieokreślona |
| Mediana |
|
| Moda |
|
| Wariancja |
nieokreślona |
| Współczynnik skośności |
nieokreślona |
| Kurtoza |
nieokreślona |
| Entropia |
|
| Funkcja tworząca momenty |
nieokreślona |
| Funkcja charakterystyczna |
|
| Odkrywca | |
Rozkład Cauchy’ego (zwany również w optyce rozkładem Lorentza, a w fizyce jądrowej rozkładem Breita-Wignera) to rozkład prawdopodobieństwa typu ciągłego.
- Momenty zwykłe i centralne (czyli m.in. wartość oczekiwana i wariancja) rozkładu są niezdefiniowane – odpowiednie całki rozbiegają się do nieskończoności. Oznacza to też m.in., że nie można zdefiniować kurtozy i skośności.
- Jeśli niezależne zmienne losowe X i Y mają standardowy rozkład normalny, to zmienna X/Y ma rozkład Cauchy’ego z parametrami x0 = 0 i γ = 1
Zobacz też
- rozkład zmiennej losowej
- przegląd zagadnień z zakresu statystyki
Linki zewnętrzne
- Eric W. Weisstein, Cauchy Distribution, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2023-08-30].
 Cauchy distribution (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-08-30].
Cauchy distribution (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-08-30].