Rozkład dwumianowy
Funkcja rozkładu prawdopodobieństwa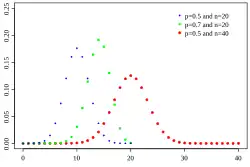 | |
Dystrybuanta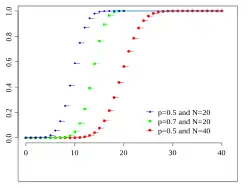 Kolory odpowiadają wykresowi powyżej | |
| Parametry |
liczba prób (liczba całkowita) |
|---|---|
| Nośnik |
|
| Funkcja rozkładu prawdopodobieństwa |
|
| Dystrybuanta |
|
| Wartość oczekiwana (średnia) |
|
| Mediana |
jedna z |
| Moda |
|
| Wariancja |
|
| Współczynnik skośności |
|
| Kurtoza |
|
| Entropia |
|
| Funkcja tworząca momenty |
|
| Funkcja charakterystyczna |
|
| Odkrywca | |
Rozkład dwumianowy (w Polsce zwany też rozkładem Bernoulliego, choć w krajach anglojęzycznych termin Bernoulli distribution odnosi się do rozkładu zero-jedynkowego) – dyskretny rozkład prawdopodobieństwa opisujący liczbę sukcesów w ciągu niezależnych prób, z których każda ma stałe prawdopodobieństwo sukcesu równe Pojedynczy eksperyment nosi nazwę próby Bernoulliego.
Innym rozkładem, który opisuje liczbę sukcesów w ciągu prób, jest rozkład hipergeometryczny. W tym przypadku jednak próby nie są niezależne (próba bez zwracania).
Jeśli i są dwiema niezależnymi zmiennymi losowymi o rozkładzie dwumianowym, wtedy ich suma jest zmienną losową o rozkładzie dwumianowym danym wzorem:
W zależności od wartości parametrów rozkład dwumianowy można przybliżać innymi z rozkładów:
- Jeśli zarówno jak i są większe od 5, wtedy rozkład dwumianowy można przybliżać rozkładem normalnym[1]:
- czyli
- Jeśli jest duże, a jest małe (czyli ma umiarkowanie dużą wartość), dobrym przybliżeniem rozkładu dwumianowego jest rozkład Poissona z parametrem
Zobacz też
Przypisy
- ↑ 6.4: Normal Approximation to the Binomial Distribution [online], Statistics LibreTexts, 11 października 2020 [dostęp 2024-06-11] (ang.).
Bibliografia
- Rozkład po raz pierwszy wprowadzony w pracy:
- George Udny Yule: An Introduction to the Theory of Statistics. Londyn: Griffin, 1911.
Linki zewnętrzne
 Binomial distribution (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2025-04-23].
Binomial distribution (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2025-04-23].