Rozkład chi kwadrat
Gęstość prawdopodobieństwa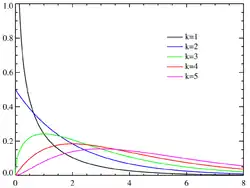 | |
Dystrybuanta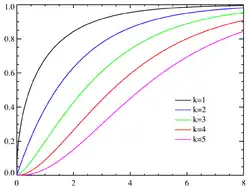 Kolory odpowiadają wykresowi powyżej | |
| Parametry |
stopni swobody |
|---|---|
| Nośnik |
|
| Gęstość prawdopodobieństwa |
|
| Dystrybuanta |
|
| Wartość oczekiwana (średnia) |
|
| Mediana |
około |
| Moda |
|
| Wariancja |
|
| Współczynnik skośności |
|
| Kurtoza |
|
| Entropia |
|
| Funkcja tworząca momenty |
|
| Funkcja charakterystyczna |
|
| Odkrywca | |
Rozkład chi kwadrat (zapisywany także jako ) – rozkład zmiennej losowej, która jest sumą kwadratów niezależnych zmiennych losowych o standardowym rozkładzie normalnym. Liczbę naturalną nazywa się liczbą stopni swobody rozkładu zmiennej losowej.
Jeżeli ciąg niezależnych zmiennych losowych oraz:
to:
czyli słownie: Zmienna losowa ma rozkład chi kwadrat o stopniach swobody.
Rozkład chi kwadrat ma duże znaczenie w statystyce, między innymi w teście chi-kwadrat, który wziął od niego swoją nazwę.
Linki zewnętrzne
 Chi-squared distribution (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2025-04-23].
Chi-squared distribution (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2025-04-23].