Rozkład beta
Gęstość prawdopodobieństwa
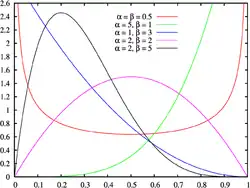 |
Dystrybuanta
 |
| Parametry |
 parametr kształtu (liczba rzeczywista) parametr kształtu (liczba rzeczywista)
 parametr kształtu (liczba rzeczywista) parametr kształtu (liczba rzeczywista)
|
| Nośnik |
![{\displaystyle x\in [0;1]}](./745b7ffd7926726b5eab739912ec7e702d9fed96.svg)
|
| Gęstość prawdopodobieństwa |

|
| Dystrybuanta |
 [a] [a]
|
| Wartość oczekiwana (średnia) |

|
| Moda |
 dla dla 
|
| Wariancja |

|
| Współczynnik skośności |

|
| Kurtoza |

|
| Entropia |
   
|
| Funkcja tworząca momenty |

|
| Funkcja charakterystyczna |
;\alpha +\beta ;i\,t)}
 |
| Odkrywca |
Corrado Gini (1911) |
Rozkład beta – rodzina ciągłych rozkładów prawdopodobieństwa zadana za pomocą funkcji gęstości

gdzie:
 – zmienna,
– zmienna, ![{\displaystyle x\in [0,1];}](./bb3d7ddb668bc2be7edfa24a90c7bd4047db50df.svg)
 – parametry rozkładu, tzw. parametry kształtu,
– parametry rozkładu, tzw. parametry kształtu, – stała zależna od
– stała zależna od  i
i  normująca rozkład do 1, tj.
normująca rozkład do 1, tj.



gdzie:
 – funkcja beta,
– funkcja beta, – funkcja gamma.
– funkcja gamma.
Gdy  to rozkład beta przyjmuje postać rozkładu jednostajnego.
to rozkład beta przyjmuje postać rozkładu jednostajnego.
Momenty zwykłe zmiennej o rozkładzie beta wynoszą:

Właściwości
Miary tendencji centralnej
Średnia
Wartość oczekiwana rozkładu beta jest funkcją stosunku parametrów  i
i  [1]:
[1]:
![{\displaystyle {\begin{aligned}\mu =\operatorname {E} [X]&=\int _{0}^{1}xf(x;\alpha ,\beta )\,dx\\&=\int _{0}^{1}x\,{\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}\,dx\\&={\frac {\alpha }{\alpha +\beta }}\\&={\frac {1}{1+{\frac {\beta }{\alpha }}}}.\end{aligned}}}](./3c01f17c920a90ad971a083ad32230d7cc658450.svg)
Jeśli oba parametry są równe,  rozkład jest symetryczny ze średnią
rozkład jest symetryczny ze średnią  Wraz z dążeniem proporcji parametrów
Wraz z dążeniem proporcji parametrów  i
i  do wartości nieskończonych lub nieskończenie małych, rozkład staje się prawo- lub lewoskośny, ze średnią dążącą do granic przedziału
do wartości nieskończonych lub nieskończenie małych, rozkład staje się prawo- lub lewoskośny, ze średnią dążącą do granic przedziału ![{\displaystyle [0,1]{:}}](./d02a400c2c0dcc495595056e687125247396d9fe.svg)


Dominanta
Maksimum lub minimum rozkładu beta wyraża funkcja[1]:

Jeśli oba parametry są mniejsze od zera,  wartość funkcji wyznacza minimum rozkładu.
wartość funkcji wyznacza minimum rozkładu.
Uwagi
- ↑

gdzie:
 – niekompletna funkcja beta.
– niekompletna funkcja beta.
Przypisy
- 1 2 3 Chapter 21: Beta Distributions, [w:] Kotz i inni, Continuous univariate distributions, Wiley, 1995, ISBN 978-0-471-58494-0, OCLC 29428092 . Brak numerów stron w książce
Bibliografia
- Rozkład po raz pierwszy wprowadzony w pracy:
- Corrado Gini: Considerazioni sulle probabilita a posteriori e applicazioni al rapporto dei sessi nelle nascite umane. Studi Economico-Giuridici della Universita de Cagliari, Anno III, 1911, s. 133–171.
Rozkłady statystyczne
| Rozkłady ciągłe |
|
|---|
| Rozkłady dyskretne |
|
|---|

