Rozkład Fishera-Tippetta
Gęstość prawdopodobieństwa
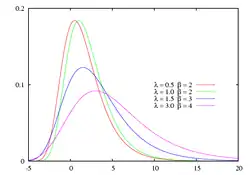
Funkcja gęstości prawdopodobieństwa rozkładu dla różnych wartości parametrów  i i  |
Dystrybuanta
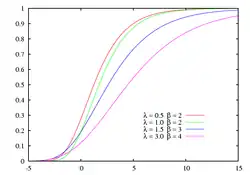
Dystrybuanta rozkładu dla różnych wartości parametrów  i i  |
| Parametry |
 parametr położenia (liczba rzeczywista) parametr położenia (liczba rzeczywista)
 parametr skali (liczba rzeczywista) parametr skali (liczba rzeczywista)
|
| Nośnik |
;+\infty )}
 |
| Gęstość prawdopodobieństwa |

gdzie ![{\displaystyle z=\exp \left[-{\frac {x-\lambda }{\beta }}\right]}](./6c0a99a4bfbd2e2721fbd1d5a36255c516ffd315.svg)
|
| Dystrybuanta |
![{\displaystyle \exp(-\exp[-(x-\lambda )/\beta ])}](./f2dca59d261dc61b2ce94a11d8ac9d85f10e3996.svg)
|
| Wartość oczekiwana (średnia) |

|
| Mediana |

|
| Moda |

|
| Wariancja |

|
| Współczynnik skośności |

|
| Kurtoza |

|
| Funkcja tworząca momenty |

|
| Funkcja charakterystyczna |

|
Rozkład Fishera-Tippetta – rozkład zmiennej losowej służący do wyznaczania ekstremalnych wartości zmiennej losowej w pewnym przedziale czasu. Większość losowych zjawisk naturalnych (takich jak temperatura otoczenia, prędkość wiatru) daje się dobrze opisywać tym rozkładem.
Rozkład Gumbela jest szczególnym przypadkiem rozkładu Fishera-Tippetta, dla:

Rozkłady statystyczne
| Rozkłady ciągłe |
|
|---|
| Rozkłady dyskretne |
|
|---|

