rozkład χ
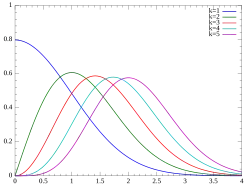
Gęstość prawdopodobieństwa
 |
| Parametry |
A, B, ν |
| Gęstość prawdopodobieństwa |

|
| Dystrybuanta |

|
| Wartość oczekiwana (średnia) |

|
| Mediana |
nie może być wyrażona za pomocą funkcji elementarnych |
| Moda |

|
| Wariancja |
![{\displaystyle B^{2}\left[\nu -{\frac {2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)}{\Gamma ^{2}\left({\frac {\nu }{2}}\right)}}\right]}](./9aad4d6f4a2afe31660064f221562081f8accfa7.svg)
|
| Współczynnik skośności |
![{\displaystyle {\frac {{\sqrt {2}}\left[4\Gamma ^{3}\left({\frac {\nu +1}{2}}\right)+\Gamma ^{2}\left({\frac {\nu }{2}}\right)\left(2\Gamma \left({\frac {\nu +3}{2}}\right)-3\nu \Gamma \left({\frac {\nu +1}{2}}\right)\right)\right]}{\Gamma ^{3}\left({\frac {\nu }{2}}\right)\left[\nu -{\frac {2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)}{\Gamma ^{2}\left({\frac {\nu }{2}}\right)}}\right]^{\frac {3}{2}}}}}](./ce69ba66d5c37168808887c356009f20206ca37a.svg)
|
| Kurtoza |
![{\displaystyle {\frac {2\nu (1-\nu )\Gamma ^{4}\left({\frac {\nu }{2}}\right)-24\Gamma ^{4}\left({\frac {\nu +1}{2}}\right)}{\left[\nu \Gamma ^{2}\left({\frac {\nu }{2}}\right)-2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)\right]^{2}}}+}](./f38cae09627de3f2065b670e153e31bea417c0c5.svg)
![{\displaystyle +{\frac {8(2\nu -1)\Gamma ^{2}\left({\frac {\nu }{2}}\right)\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)}{\left[\nu \Gamma ^{2}\left({\frac {\nu }{2}}\right)-2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)\right]^{2}}}}](./a2402e534ef694a1d0d26af95abc92d91ff0101b.svg)
|
Rozkład chi (zapisywany jako rozkład χ) to rozkład prawdopodobieństwa typu ciągłego.
Funkcja gęstości prawdopodobieństwa tego rozkładu dana jest wzorem:

gdzie  to parametry rozkładu, zaś Γ oznacza funkcję gamma.
to parametry rozkładu, zaś Γ oznacza funkcję gamma.
Parametr  nazywany jest liczbą stopni swobody rozkładu, musi być liczbą większą od 0.
nazywany jest liczbą stopni swobody rozkładu, musi być liczbą większą od 0.
Dystrybuanta tego rozkładu ma postać:

Własności:
skośność:
![{\displaystyle {\frac {{\sqrt {2}}\left[4\Gamma ^{3}\left({\frac {\nu +1}{2}}\right)+\Gamma ^{2}\left({\frac {\nu }{2}}\right)\left(2\Gamma \left({\frac {\nu +3}{2}}\right)-3\nu \Gamma \left({\frac {\nu +1}{2}}\right)\right)\right]}{\Gamma ^{3}\left({\frac {\nu }{2}}\right)\left[\nu -{\frac {2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)}{\Gamma ^{2}\left({\frac {\nu }{2}}\right)}}\right]^{\frac {3}{2}}}}}](./ce69ba66d5c37168808887c356009f20206ca37a.svg)
kurtoza:
![{\displaystyle {\frac {2\nu (1-\nu )\Gamma ^{4}\left({\frac {\nu }{2}}\right)-24\Gamma ^{4}\left({\frac {\nu +1}{2}}\right)}{\left[\nu \Gamma ^{2}\left({\frac {\nu }{2}}\right)-2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)\right]^{2}}}+}](./f38cae09627de3f2065b670e153e31bea417c0c5.svg)
![{\displaystyle +{\frac {8(2\nu -1)\Gamma ^{2}\left({\frac {\nu }{2}}\right)\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)}{\left[\nu \Gamma ^{2}\left({\frac {\nu }{2}}\right)-2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)\right]^{2}}}}](./a2402e534ef694a1d0d26af95abc92d91ff0101b.svg)
Specjalne przypadki:
 – rozkład półnormalny
– rozkład półnormalny – rozkład Rayleigha
– rozkład Rayleigha – rozkład Maxwella
– rozkład Maxwella
Zobacz też
Rozkłady statystyczne
| Rozkłady ciągłe |
|
|---|
| Rozkłady dyskretne |
|
|---|
