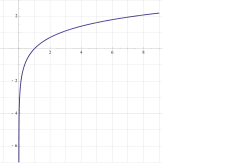
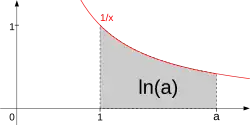
Logarytm jako granica
Logarytm naturalny można zdefiniować również jako pewną granicę:

Dowód
Oznaczmy:
| |  |
|
(1) |
Wtedy  Logarytmując obustronnie przy podstawie
Logarytmując obustronnie przy podstawie  otrzymujemy:
otrzymujemy:


Mnożąc obustronnie przez (1), otrzymujemy:

Teraz należy wykazać, że przy  mianownik dąży do jednego. Otóż:
mianownik dąży do jednego. Otóż:

Gdy więc x dąży do zera, mianownik powyższego ułamka dąży do zera, więc z dąży do nieskończoności. Zatem wobec ciągłości logarytmu:

Wyrażenie  w mianowniku dąży do
w mianowniku dąży do  więc mianownik jest równy
więc mianownik jest równy  co było do okazania.
co było do okazania.
Pochodna logarytmu naturalnego
Ogólnie pochodna logarytmu wyrażona jest wzorem:

Czyli dla logarytmu naturalnego, gdzie  otrzymujemy:
otrzymujemy: 
Wartości pochodnych wyższych rzędów możemy wyznaczyć ze wzoru na  -tą pochodną logarytmu naturalnego, czyli:
-tą pochodną logarytmu naturalnego, czyli: 
Własności
 dla
dla 
 dla
dla 
 dla
dla 
Powyższe własności jednoznacznie definiują funkcję :(0,\infty )\to \mathbb {R} }

 dla
dla 
- Jeśli ciąg
 to:
to:


 dla
dla 




 dla
dla 
 dla
dla