Kwadratura koła

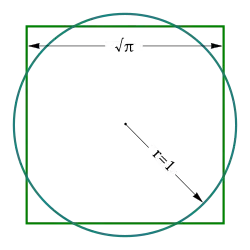
Kwadratura koła – problem polegający na skonstruowaniu kwadratu, którego pole równe jest polu danego koła^[1] przy użyciu wyłącznie cyrkla i linijki bez podziałki^[2]. Jest to jeden z trzech wielkich problemów starożytnej matematyki greckiej (obok trysekcji kąta i podwojenia sześcianu), sformułowany przez szkołę pitagorejską.

Konstrukcja taka jest niewykonalna^[2] – wynika to z twierdzenia udowodnionego w roku 1837 przez Pierre’a Wantzela oraz faktu wykazanego w 1882 roku przez Ferdinanda Lindemanna, że π jest liczbą przestępną^[2].

Pierwsze próby kwadratury koła sięgają Starożytnego Egiptu, opisane zostały jako problem 48 w Papirusie Rhinda, gdzie opisana została aproksymacja kwadratury koła^[3].

Kwadratura koła jest bezpośrednio związana z rektyfikacją okręgu: gdyby jedna z tych konstrukcji była wykonalna, oznaczałoby to, że wykonalna jest także druga.

Określenie „kwadratura koła” funkcjonuje również w języku potocznym i oznacza coś niewykonalnego, z góry skazanego na niepowodzenie.

• kwadratura figury geometrycznej
• księżyce Hipokratesa

• MarekM. Kordos MarekM., Rektyfikacja i kwadratura według Archimedesa, „Delta”, marzec 2018, ISSN 0137-3005 [dostęp 2024-11-02] .
• Eric W.E.W. Weisstein Eric W.E.W., Circle Squaring, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2024-03-07].
• John J.J.J. O’Connor John J.J.J., Edmund F.E.F. Robertson Edmund F.E.F., Squaring the circle, MacTutor History of Mathematics archive [zarchiwizowane 2012-12-23]  (ang.).