Trójkąt eulerowski

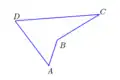
Trójkąt eulerowski – trójkąt sferyczny spełniający warunek: każdy bok i każdy kąt ma miarę mniejszą niż 180°. Figura ta ma szczególne znaczenie w geodezji wyższej, pozwala w łatwy sposób obliczyć m.in. współrzędne punktów na sferze w oparciu o znane współrzędne punktu będącego jednym z wierzchołków.
| relacje między |
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| figury definiowane okręgami |
| ||||||||||||
| twierdzenia |
| ||||||||||||
| problemy (zadania) |
| ||||||||||||
| opis analityczny |
| ||||||||||||
| narzędzia | |||||||||||||
| inne pojęcia | |||||||||||||
| uogólnienia |
| ||||||||||||
| powiązane nauki |
| ||||||||||||
| badacze |
|


| pojęcia definiujące | |||||||
|---|---|---|---|---|---|---|---|
| trójkąty |
| ||||||
| czworokąty |
| ||||||
| inne grupy z ustaloną liczbą boków |
| ||||||
| wielokąty foremne |
| ||||||
| wielokąty gwiaździste |
| ||||||
| inne | |||||||
| relacje dwuczłonowe między wielokątem a |
| ||||||
| obiekty nazywane jak wielokąty |
| ||||||
| uogólnienia |
|

| przykłady i ich części |
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| relacje między kulą a innymi bryłami | |||||||||||||
| krzywe tworzone przekrojami brył obrotowych |
| ||||||||||||
| inne krzywe na bryłach obrotowych |
| ||||||||||||
| powiązane układy współrzędnych | |||||||||||||
| twierdzenia | |||||||||||||
| powiązane powierzchnie |
| ||||||||||||
| powiązane nauki |
| ||||||||||||
| badacze |
|

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.