Lemat Zassenhausa

Lemat Zassenhausa (także: lemat motyla) – techniczny wynik teorii grup dotyczący kraty podgrup danej grupy, w uogólnieniach również kraty podmodułów ustalonego modułu lub, ogólnie, dowolnej kraty modularnej^[1]. „Motyla” można dojrzeć na diagramie Hassego grup biorących udział w twierdzeniu.

Hans Julius Zassenhaus udowodnił lemat, mając na celu podanie czytelniejszej postaci dowodu twierdzenia Shreiera; można go też uzyskać z ogólniejszego wyniku znanego jako twierdzenie Goursata dla rozmaitości Goursata (których przykładem są grupy), wykorzystując prawo modularności Dedekinda^[2]. Twierdzenie zachodzi w szczególności również dla grup z operatorami: w sformułowaniu wystarczy zamienić podgrupy normalne na podgrupy stabilne.

Lemat

Niech $G$ będzie grupą, a $A$ oraz $C$ jej podgrupami; ponadto niech $B\trianglelefteq A$ oraz $D\trianglelefteq C$ będą podgrupami normalnymi, wówczas

B(A\cap D)\trianglelefteq B(A\cap C)\quad {\text{oraz}}\quad D(B\cap C)\trianglelefteq D(A\cap C)

i ma miejsce izomorfizm

B(A\cap C){\big /}B(A\cap D)\simeq D(A\cap C){\big /}D(B\cap C).

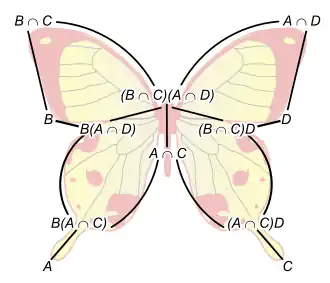
Dowód

Niech ${\widehat {UV}}:=U\cap V.$ Ponieważ $B\trianglelefteq A,$ to^[a] $B\cap C\trianglelefteq A\cap C,$ czyli ${\widehat {BC}}\trianglelefteq {\widehat {AC}};$ podobnie dla $C\trianglelefteq D$ jest ${\widehat {AD}}\trianglelefteq {\widehat {AC}}.$ Jako że ${\widehat {BC}}\trianglelefteq {\widehat {AC}}$ oraz ${\widehat {AD}}\trianglelefteq {\widehat {AC}},$ zapisując dla zwięzłości $E={\widehat {BC}}\,{\widehat {AD}}={\widehat {AD}}\,{\widehat {BC}},$ to zachodzi $E\trianglelefteq {\widehat {AC}}$ (jako iloczyn prosty, zob. iloczyn kompleksowy).

Ponieważ $E\trianglelefteq {\widehat {AC}}\leqslant A$ oraz $B\trianglelefteq A,$ to^[b]

BE\trianglelefteq B{\widehat {AC}}\quad {\text{oraz}}\quad B{\widehat {AC}}/BE\simeq {\widehat {AC}}/E(B\cap {\widehat {AC}}).\qquad (1)

Teraz $BE=B({\widehat {BC}}\,{\widehat {AD}})=(B{\widehat {BC}}){\widehat {AD}}=B{\widehat {AD}}$ oraz $E(B\cap {\widehat {AC}})=E$ (ponieważ $B\cap {\widehat {AC}}={\widehat {BC}}\subseteq E$ ), a więc z (1) wynika

B{\widehat {AD}}\trianglelefteq B{\widehat {AC}}\quad {\text{oraz}}\quad B{\widehat {AC}}/B{\widehat {AD}}\simeq {\widehat {AC}}/E.\qquad (2)

Powtarzając to samo rozumowanie dla $A,B$ zastąpionymi odpowiednio $C,D,$ uzyskuje się

D{\widehat {BC}}\trianglelefteq D{\widehat {AC}}\quad {\text{oraz}}\quad D{\widehat {AC}}/D{\widehat {BC}}\simeq {\widehat {AC}}/E.\qquad (3)

Teza wynika z połączenia (2) oraz (3).

Zobacz też

Uwagi

↑ Lemat 1. Niech $B\trianglelefteq A\leqslant G$ oraz $C\leqslant G.$ Wówczas $B\cap C\trianglelefteq A\cap C$ oraz $A\cap C/B\cap C\simeq B(C\cap A)/B.$
Dowód. Drugie twierdzenie o izomorfizmie mówi, że jeśli $G$ jest grupą, a $H\trianglelefteq G$ oraz $K\leqslant G,$ to $H\cap K\trianglelefteq K$ oraz $K/H\cap K$ jest izomorficzna z $HK/H.$
Stosując to twierdzenie dla $G,H,K$ zastąpionych odpowiednio $A,B,A\cap C,$ otrzymuje się $B\cap (A\cap C)\trianglelefteq A\cap C$ oraz $A\cap C/B\cap (A\cap C)\simeq B(A\cap C)/B.$ Skoro $B\cap (A\cap C)=B\cap C,$ a $B(A\cap C)=B(C\cap A),$ to zachodzi teza.
↑ Lemat 2. Niech $A\trianglelefteq C\leqslant G$ oraz $B\trianglelefteq G.$ Wówczas $BA\trianglelefteq BC$ oraz $BC/BA\simeq C/A(B\cap C).$
Dowód. Ponieważ $B\trianglelefteq G,$ to wiadomo, że $AB=BA\leqslant G$ oraz $CB=BC\leqslant G.$ Zatem $BA\leqslant BC.$ Należy dowieść, że $BA$ jest normalna w $BC.$ Zauważając, że $B\leqslant BA\leqslant N_{G}(BA)$ (zob. normalizator), otrzymuje się $(BA)^{b}=BA$ dla wszystkich $b\in B$ (zob. sprzężenie i podgrupa normalna). Wtedy, dla dowolnych $b\in B,\,c\in C,$ jest $(BA)^{bc}=[(BA)^{b}]^{c}=(BA)^{c}=B^{c}A^{c}=BA^{c}=BA,$ ponieważ $B\triangleleft G$ oraz $A\trianglelefteq C.$ Zatem $(BA)^{x}=BA$ dla wszystkich $x\in BC$ oraz $BA\trianglelefteq BC.$ Z drugiego twierdzenia o izomorfizmie z $BC,BA,C$ odpowiednio w miejscach $G,H,K$ otrzymuje się $AB\cap C\trianglelefteq C$ oraz $C/AB\cap C\simeq C(AB)/AB.$ Ponieważ $AB\cap C=A(B\cap C)$ oraz $C(AB)=(CA)B=CB=BC,$ to izomorfizm ten oznacza, że $C/A(B\cap C)\simeq BC/BA.$

Przypisy

↑ Zob. Pierce, s. 27, ćw. 1.
↑ The Butterfly and the Serpent. W: J. Lambek: Logic and Algebra. Aldo Ursini, Paulo Agliano (red.). CRC Press, 1996, s. 161–180. ISBN 978-0-8247-9606-8.

Bibliografia

R.S. Pierce: Associative algebras. Springer, 1982, s. 27. ISBN 0-387-90693-2.
Serge Lang: Algebra. Wyd. III (popr.). Springer-Verlag, s. 20–21, seria: Graduate Texts in Mathematics. ISBN 978-0-387-95385-4.
Hans Zassenhaus. Zum Satz von Jordan–Hölder–Schreier. „Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg”. 10, s. 106–108, 1934.

[lemat1-3] Lemat 1. Niech $B\trianglelefteq A\leqslant G$ oraz $C\leqslant G.$ Wówczas $B\cap C\trianglelefteq A\cap C$ oraz $A\cap C/B\cap C\simeq B(C\cap A)/B.$
Dowód. Drugie twierdzenie o izomorfizmie mówi, że jeśli $G$ jest grupą, a $H\trianglelefteq G$ oraz $K\leqslant G,$ to $H\cap K\trianglelefteq K$ oraz $K/H\cap K$ jest izomorficzna z $HK/H.$
Stosując to twierdzenie dla $G,H,K$ zastąpionych odpowiednio $A,B,A\cap C,$ otrzymuje się $B\cap (A\cap C)\trianglelefteq A\cap C$ oraz $A\cap C/B\cap (A\cap C)\simeq B(A\cap C)/B.$ Skoro $B\cap (A\cap C)=B\cap C,$ a $B(A\cap C)=B(C\cap A),$ to zachodzi teza.

[lemat2-4] Lemat 2. Niech $A\trianglelefteq C\leqslant G$ oraz $B\trianglelefteq G.$ Wówczas $BA\trianglelefteq BC$ oraz $BC/BA\simeq C/A(B\cap C).$
Dowód. Ponieważ $B\trianglelefteq G,$ to wiadomo, że $AB=BA\leqslant G$ oraz $CB=BC\leqslant G.$ Zatem $BA\leqslant BC.$ Należy dowieść, że $BA$ jest normalna w $BC.$ Zauważając, że $B\leqslant BA\leqslant N_{G}(BA)$ (zob. normalizator), otrzymuje się $(BA)^{b}=BA$ dla wszystkich $b\in B$ (zob. sprzężenie i podgrupa normalna). Wtedy, dla dowolnych $b\in B,\,c\in C,$ jest $(BA)^{bc}=[(BA)^{b}]^{c}=(BA)^{c}=B^{c}A^{c}=BA^{c}=BA,$ ponieważ $B\triangleleft G$ oraz $A\trianglelefteq C.$ Zatem $(BA)^{x}=BA$ dla wszystkich $x\in BC$ oraz $BA\trianglelefteq BC.$ Z drugiego twierdzenia o izomorfizmie z $BC,BA,C$ odpowiednio w miejscach $G,H,K$ otrzymuje się $AB\cap C\trianglelefteq C$ oraz $C/AB\cap C\simeq C(AB)/AB.$ Ponieważ $AB\cap C=A(B\cap C)$ oraz $C(AB)=(CA)B=CB=BC,$ to izomorfizm ten oznacza, że $C/A(B\cap C)\simeq BC/BA.$

[1] Zob. Pierce, s. 27, ćw. 1.

[2] The Butterfly and the Serpent. W: J. Lambek: Logic and Algebra. Aldo Ursini, Paulo Agliano (red.). CRC Press, 1996, s. 161–180. ISBN 978-0-8247-9606-8.

[1]

[2]

[a]

[b]